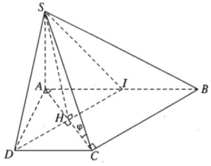
a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?
b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng \(\left( Q \right)\) và mặt đất \(\left( P \right)\).

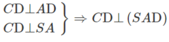
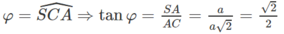
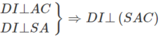
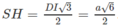 .
. 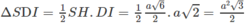

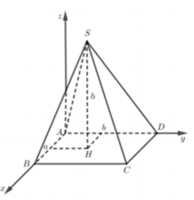
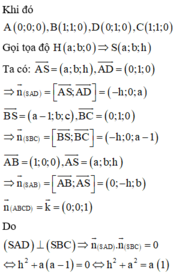
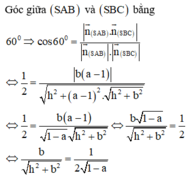
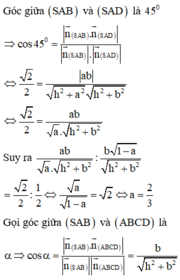
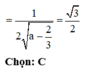
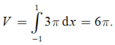
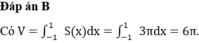
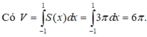
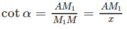
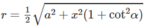
a: Có thể xác định được bằng cách bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh.
b: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
Khi đặt thiết bị lên mp nghiêng (Q) thì ta sẽ có:
\(OM\perp\left(Q\right);ON\perp\left(P\right)\)
\(OM\subset\left(P\right),ON\subset\left(Q\right)\)
=>\(\widehat{\left(P\right),\left(Q\right)}=\widehat{\left(OM;ON\right)}=\widehat{MON}=90^0\)