Nhắc lại rằng, mức cường độ âm \(L\) được tính bằng công thức \(L = 10\log \left( {\frac{I}{{{I_0}}}} \right)\left( {dB} \right)\), trong đó \(I\) là cường độ của âm tính bằng \(W/{m^2}\) và \({I_0} = {10^{ - 12}}W/{m^2}\).
(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)
a) Một giáo viên đang giảng bài trong lớp học có mức cường độ âm là 50 dB. Cường độ âm của giọng nói giáo viên bằng bao nhiêu?
b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75 dB đến 90 dB. Cường độ âm trong nhà xưởng này thay đổi trong khoảng nào?


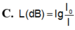
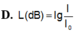
a, Ta có:
\(L=50\Leftrightarrow10log\left(\dfrac{I}{I_0}\right)=50\\ \Leftrightarrow\dfrac{I}{I_0}=10^5\\ \Leftrightarrow I=I_0\cdot10^5=10^{-12}\cdot10^5=10^{-7}\left(W/m^2\right)\)
Vậy cường độ âm của giọng nói giáo viên là \(I=10^{-7}\left(W/m^2\right)\)
b, Ta có:
\(75\le L\le90\Leftrightarrow75\le10log\left(\dfrac{I}{I_0}\right)\le90\Leftrightarrow10^{7,5}\le\dfrac{I}{10^{-12}}\le10^9\\ \Leftrightarrow10^{-4,5}\le I\le10^{-3}\\ \Leftrightarrow3,16\cdot10^{-5}\le I\le10^{-3}\)
Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng \(3,16\cdot10^{-5}\left(W/m^2\right)\) đến \(10^{-3}\left(W/m^2\right)\)