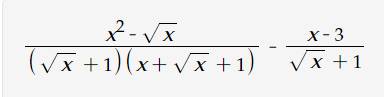
rút gọn và tìm gtln của nó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 9 2018
\(A=4\left(x+2\right)-\left(2x+1\right)\left(2x-1\right)\)
\(A=4x+8-4x^2+1\)
\(A=-\left(4x^2-4x+4\right)+13\)
\(A=-\left(2x+2\right)^2+13\)
Vì \(-\left(2x+2\right)^2\le0\forall x\)
\(\Rightarrow-\left(2x+2\right)^2+13\le13\forall x\)
\(\Rightarrow A_{max}=13\)khi và chỉ khi \(-\left(2x+2\right)^2=0\Rightarrow x=-1\)
23 tháng 10 2021
b: Theo đề, ta có:
\(\dfrac{a}{74-a}=\dfrac{23}{51}\)
\(\Leftrightarrow51a=1702-23a\)
\(\Leftrightarrow74a=1702\)
hay a=23
PT
0
NT
0
5 tháng 4 2022
a: Khi x=4 thì \(A=\left(\dfrac{2+2}{2+1}-\dfrac{2\cdot2-2}{2-1}\right)\cdot\left(4-1\right)=\dfrac{1}{3}\cdot3=1\)
b: \(A=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-2\right)\cdot\left(x-1\right)\)
\(=\dfrac{\sqrt{x}+2-2\sqrt{x}-2}{\sqrt{x}+1}\cdot\left(x-1\right)=-\sqrt{x}\left(\sqrt{x}-1\right)\)
LH
3
M
1 tháng 2 2015
sau khi rút gọn số đo thị được 8/5. vậy số bé là 5 phần, số lớn 8 phần.
vẽ sơ đồ hiệu ti.
hiệu số phần = nhau là:8-5=3
số bé là: 15:3x5=25
số lớn là:25+15=40
đáp số:SB:25;SL:40
1 tháng 2 2015
sau khi rút gọn số đo thị được 8/5. vậy số bé là 5 phần, số lớn 8 phần.
vẽ sơ đồ hiệu ti.
hiệu số phần = nhau là:8-5=3
số bé là: 15:3x5=25
số lớn là:25+15=40
đáp số:SB:25;SL:40
17 tháng 5 2021
`A=(1/(x-sqrtx)+1/(sqrtx-1)):(sqrtx+1)/(sqrtx-1)^2`
`=((sqrtx+1)/(x-sqrtx)).(sqrtx-1)^2/(sqrtx+1)`
`=(sqrtx-1)^2/(x-sqrtx)`
`=(sqrtx-1)/sqrtx`
ĐKXĐ: x>=0
\(A=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x-3}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}-\dfrac{x-3}{\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}-x+3}{\sqrt{x}+1}=\dfrac{-\sqrt{x}+3}{\sqrt{x}+1}\)
\(=\dfrac{-\sqrt{x}-1+4}{\sqrt{x}+1}=-1+\dfrac{4}{\sqrt{x}+1}\)
\(\dfrac{4}{\sqrt{x}+1}< =\dfrac{4}{1}=4\)
=>\(\dfrac{4}{\sqrt{x}+1}-1< =4-1=3\)
Dấu = xảy ra khi x=0