X2 y4 _ 16xy3 +68y2_4xy+x2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 7 2023
\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2yz+2xz\) Thay x+y+z=0 vào
\(\Rightarrow0=x^2+y^2+z^2+2\left(xy+yz+xz\right)\)
\(\Leftrightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\) (1)
Ta có
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2x^2y^2+2y^2z^2+2x^2z^2\) (2)
Bình phương 2 vế của (1)
\(\left(x^2+y^2+z^2\right)^2=4\left(xy+yz+xz\right)^2\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2+2xy^2z+2xyz^2+2x^2yz\right)\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left[x^2y^2+y^2z^2+x^2z^2+2xyz\left(x+y+z\right)\right]\)
Do x+y+z=0 nên
\(\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2\right)\)
\(\Rightarrow\dfrac{\left(x^2+y^2+z^2\right)^2}{2}=2x^2y^2+2y^2z^2+2x^2z^2\) (3)
Thay (3) vào (2)
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+\dfrac{\left(x^2+y^2+z^2\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4+z^4\right)=\left(x^2+y^2+z^2\right)^2\) (đpcm)
TT
0
CM
18 tháng 11 2019
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: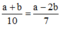 
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
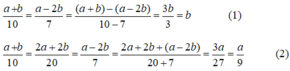
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.
HT
1
19 tháng 10 2021
\(\left(x^2+2xy\right)^2+2\left(x^2+2xy\right)y^2+y^4\)
\(=\left(x^2+2xy+y^2\right)^2\)
\(=\left(x+y\right)^4\)
16 tháng 11 2021
\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
16 tháng 11 2021
Câu 1
a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)
b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)
NH
1
4 tháng 7 2023
1: \(=\dfrac{x-1}{x^2+x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{x^2-2x+1+x^3+x^2+x^2+x+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3+3x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
2: \(=\dfrac{\left(x^2-y^2\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{\left(x-y\right)\left(x+y\right)^2}{x^2+xy+y^2}\)
28 tháng 6 2021
6) Ta có: \(x^2+2xy+y^2-x-y-12\)
\(=\left(x+y\right)^2-\left(x+y\right)-12\)
\(=\left(x+y-4\right)\left(x+y+3\right)\)
7) Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
\(=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
8) Ta có: \(4x^4-32x^2+1\)
\(=4x^4+12x^3+2x^2-12x^3-36x^2-6x+2x^2+6x+1\)
\(=2x^2\left(2x^2+6x+1\right)-6x\left(2x^2+6x+1\right)+\left(2x^2+6x+1\right)\)
\(=\left(2x^2+6x+1\right)\left(2x^2-6x+1\right)\)
9) Ta có: \(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2\)
\(=3\left[x^4+2x^2+1-x^2\right]-\left(x^2+x+1\right)^2\)
\(=3\left(x^2-x+1\right)\left(x^2+x+1\right)-\left(x^2+x+1\right)^2\)
\(=\left(x^2+x+1\right)\left(3x^2-3x+3-x^2-x-1\right)\)
\(=\left(x^2+x+1\right)\left(2x^2-4x+2\right)\)
\(=2\left(x-1\right)^2\cdot\left(x^2+x+1\right)\)
