dùng hệ thức Vi-ét để tính nhẩm các nghiệm của phương trình :
x2 - 7x + 12 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
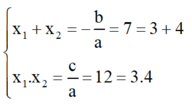
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
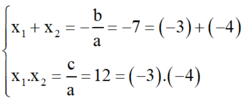
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
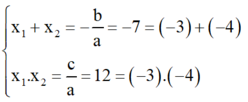
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

x2 – 7x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b2 – 4ac = (-7)2 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
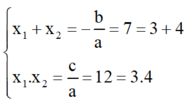
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.

Ta có: ∆ ’ = 3 2 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: 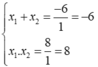
Giải ra ta được x 1 = -2, x 2 = -4

Ta có: ∆ ’ = - 6 2 -1.32 = 36 - 32 = 4 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x 1 =4, x 2 =8

Ta có: ∆ ’ = - 3 2 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: 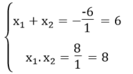
Giải ra ta được x 1 =2, x 2 =4

Ta có: ∆ = - 3 2 -4.1.(-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: 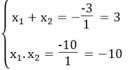
Giải ra ta được x 1 =-2, x 2 =5

Ta có: ∆ = - 3 2 -4.1.(-10)=9 +40 =49 > 0
Ta có: ∆ = 3 2 -4.1.(-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: 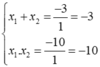
Giải ra ta được: x 1 = 2, x 2 = -5

Ta có: ∆ = - 7 2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 =-b/a =7/2 ; x 1 x 2 =c/a =2/2 =1
\(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=7\\x_1x_2=12\end{cases}\Leftrightarrow}x_{1,2}=3;4\)
Hoặc x=3 hoặc x=4