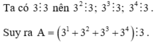Câu 1. Không thực hiện phép tính, chứng minh rằng 𝐴 = 15.16 𝑐ℎ𝑖𝑎 ℎế𝑡 𝑐ℎ𝑜 40
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Đúng(0)
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(B=2024\cdot14\)
\(B=2\cdot1012\cdot14\)
\(B=28\cdot1012\)
Vậy B chia hết cho 28
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(C=111111\cdot18\)
\(C=3\cdot7\cdot11\cdot13\cdot37\cdot3^2\cdot2\)
\(C=\left(3\cdot3^2\right)\cdot\left(7\cdot11\cdot13\cdot37\cdot2\right)\)
\(C=3^3\cdot74074\)
\(C=27\cdot74074\)
Vậy C chia hết cho 27
MA
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(11^{2024}\)
\(=11^2\cdot11^{2022}\)
\(=121\cdot11^{2022}\)
Vậy \(11^{2024}\) chia hết cho \(121\)
MA
2
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(3^{2022}\)
\(=3^2\cdot3^{2020}\)
\(=3^2\cdot3^2\cdot3^{2018}\)
\(=3^4\cdot3^{2018}\)
\(=81\cdot3^{2018}\)
Vậy \(3^{2022}\) chia hết cho 81
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(A=15\cdot16\)
\(A=3\cdot5\cdot2^4\)
\(A=3\cdot5\cdot2^3\cdot2\)
\(A=2^3\cdot5\cdot3\cdot2\)
\(A=40\cdot6\)
Vậy A chia hết cho 40
26 tháng 12 2022
a) A=3+32+33+34+35+36+....+328+329+330A=3+32+33+34+35+36+....+328+329+330
⇔A=(3+32+33)+(34+35+36)+....+(328+329+330)⇔A=(3+32+33)+(34+35+36)+....+(328+329+330)
⇔A=3(1+3+32)+34(1+3+32)+....+328(1+3+32)⇔A=3(1+3+32)+34(1+3+32)+....+328(1+3+32)
⇔A=3.13+34.13+....+328.13⇔A=3.13+34.13+....+328.13
⇔A=13(3+34+....+328)⋮13(dpcm)⇔A=13(3+34+....+328)⋮13(dpcm)
b) A=3+32+33+34+35+36+....+325+326+327+328+329+330A=3+32+33+34+35+36+....+325+326+327+328+329+330
⇔A=(3+32+33+34+35+36)+....+(325+326+327+328+329+330)⇔A=(3+32+33+34+35+36)+....+(325+326+327+328+329+330)
⇔A=3(1+3+32+33+34+35)+....+325(1+3+32+33+34+35)⇔A=3(1+3+32+33+34+35)+....+325(1+3+32+33+34+35)
⇔A=3.364+....+325.364⇔A=3.364+....+325.364
⇔A=364(3+35+310+....+325)⇔A=364(3+35+310+....+325)
⇔A=52.7(3+35+310+....+325)⋮52(dpcm)
NH
1
PH
29 tháng 12 2015
Ta có:2.4.6.8.10=40.2.6.8 chia hết cho 40
mà 40 chia hết cho 40
nên 2.4.6.8.10+40 chia hết cho 4