em xin giải chi tiết bài này em cảm ơn ạaaTT
K
Khách
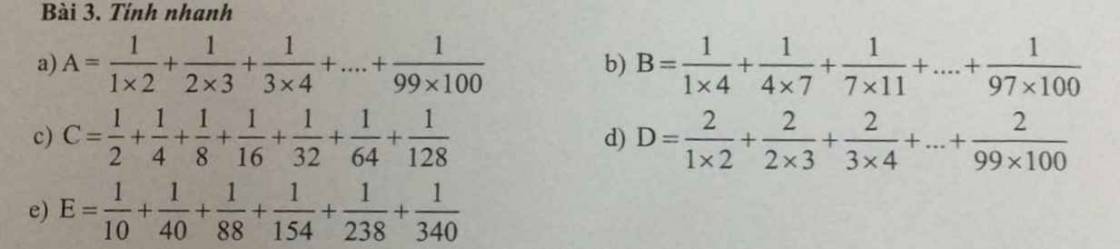
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
3
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(a,\dfrac{x}{9}=\dfrac{5}{3}\\ \Leftrightarrow x=9\cdot\dfrac{5}{3}\\ \Leftrightarrow x=15\\ b,\dfrac{17}{x}=\dfrac{85}{105}\\ \Leftrightarrow x=17\cdot\dfrac{105}{85}\\ \Leftrightarrow x=21\\ c,\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\\ \Leftrightarrow\dfrac{x}{8}=\dfrac{1}{2}\\ \Leftrightarrow x=4\\ d,\dfrac{3}{x-7}=\dfrac{27}{135}\\ \Leftrightarrow x-7=15\\ \Leftrightarrow x=22\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(e,\dfrac{75}{20-x}=\dfrac{3}{2}\times10\\ \Leftrightarrow\dfrac{75}{20-x}=15\\ \Leftrightarrow20-x=5\\ \Leftrightarrow x=15\\ f,\left(x-50\%\right)\times\dfrac{5}{3}=\dfrac{7}{4}-0,5\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{5}{4}\\ \Leftrightarrow x-\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x=\dfrac{5}{4}\\ g,\left(\dfrac{2}{15}+\dfrac{3}{35}+\dfrac{2}{63}\right):x=\dfrac{1}{18}\\ \Leftrightarrow\dfrac{2}{9}:x=\dfrac{1}{18}\\ \Leftrightarrow x=4\)
\(h,\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=0,6\times\dfrac{40}{6}\\ \Leftrightarrow\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=4\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6+4=6\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6=2\\ \Leftrightarrow x-\dfrac{1}{2}=12\\ \Leftrightarrow x=\dfrac{25}{2}\)
HH
5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 8 2023
3 ) Ngày thứ nhất cửa bán được
42 x \(\dfrac{2}{7}=12\) (bao đường)
Ngày thứ hai cửa hàng bán được
(42 - 12) x \(\dfrac{3}{5}\) = 18 (bao đường)
Cửa hàng còn lại số bao đường
42 - 12 - 18 = 12 (bao đường)
Đáp số 12 bao đường
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 8 2023
Tỉ số cam và xoài là
\(\dfrac{1}{2}:\dfrac{2}{5}=\dfrac{5}{4}\)
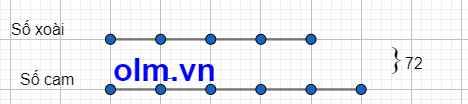
Số cam là
72: ( 5+4) x 5 = 40 (cam)
Số xoài là
72 - 40 = 32 (xoài)
Đáp số : xoài 32 quả
cam 40 quả
TD
mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
0
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
16 tháng 12 2021
\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
TT
giải chi tiết 3 bài này dùm em vs ạ 
0
LT
0
AN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2023
a.
Hệ có nghiệm duy nhất khi:
\(\dfrac{m}{2}\ne\dfrac{1}{-1}\Rightarrow m\ne-2\)
b.
Hệ có vô số nghiệm khi:
\(\dfrac{1}{1}=\dfrac{m}{-1}=\dfrac{3}{3}\Rightarrow m=-1\)
c.
Hệ vô nghiệm khi:
\(\dfrac{2}{-4}=\dfrac{-1}{2}\ne\dfrac{-m}{4}\Rightarrow m\ne2\)
NT
1
21 tháng 3 2022
\(n_{Fe}=\dfrac{5,6}{56}=0,1mol\)
\(n_S=\dfrac{4,8}{32}=0,15mol\)
\(Fe+S\underrightarrow{t^o}FeS\)
0,1 0,15 0,1
\(FeS+2HCl\rightarrow FeCl_2+H_2S\uparrow\)
0,1 0,1 0,1
\(V_Y=0,1\cdot22,4=2,24l\)
\(m_Z=m_{FeCl_2}=0,1\cdot127=12,7g\)
\(a,A=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{99\times100}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =1-\dfrac{1}{100}\\ =\dfrac{99}{100}\\ b,B=\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+...+\dfrac{1}{97\times100}\\ =\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\\ =\dfrac{1}{3}\cdot\left(1-\dfrac{1}{100}\right)\\ =\dfrac{1}{3}\cdot\dfrac{99}{100}\\ =\dfrac{33}{100}\)
\(c,C=\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{128}\\ =\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^7}\\ \Rightarrow2C=1+\dfrac{1}{2}+...+\dfrac{1}{2^6}\\ \Rightarrow2C-C=1-\dfrac{1}{2^7}\\ \Rightarrow C=\dfrac{127}{128}\)
\(d,D=\dfrac{2}{1\times2}+\dfrac{2}{2\times3}+...+\dfrac{2}{99\times100}\\ =2\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\\ =2\cdot\left(1-\dfrac{1}{100}\right)\\ =\dfrac{99}{55}\)
\(e,E=\dfrac{1}{10}+\dfrac{1}{40}+...+\dfrac{1}{340}\\ =\dfrac{1}{2\times5}+\dfrac{1}{5\times8}+...+\dfrac{1}{17\times20}\\ =\dfrac{1}{3}\cdot\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{17}-\dfrac{1}{20}\right)\\ =\dfrac{1}{3}\cdot\left(\dfrac{1}{2}-\dfrac{1}{20}\right)\\ =\dfrac{1}{3}\cdot\dfrac{9}{20}\\ =\dfrac{3}{20}\)