Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 60 cm, 30 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2015
Bài 1 :
Nửa chu vi hình chữ nhật là : 54 : 2 = 27 ( m )
Nếu giảm chiều dài 2,5 m và tăng chiều rộng 2,5 m thì được một hình vuông . Vậy lúc đầu chiều dài hơn chiều rộng : 2,5 x 2 = 5 ( m )
Chiều dài hình chữ nhật là : ( 27 + 5 ) : 2 = 16 ( m )
Chiều rộng hình chữ nhật là : 27 - 16 = 11 ( m )
Đáp số : .....
Bài 2 :
Nếu lấy 4,4 kg ở sợt thứ nhất chuyển sang sọt thứ hai thì số cam hai sọt bằng nhau . Vậy lúc đầu sọt thứ nhất hơn sot thứ hai : 4,4 x 2 = 8,8 ( kg )
Sọt thứ nhất nặng số kg là : ( 76,8 + 8,8 ) : 2 = 42,8 ( kg )
Sọt thứ hai nặng số kg là : 76,8 - 42,8 = 34 ( kg )
Đáp số : .......
QD
24 tháng 4 2017
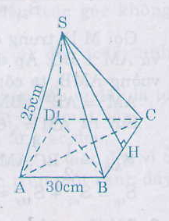
Ta có : \(d=SH=\sqrt{SB^2-BH^2}\)
\(=\sqrt{25^2-15^2}=\sqrt{400}=20\left(cm\right)\)
Diện tích xung quanh của hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).30.4.20 = 1200 (cm2)
Diện tích đáy: Sđ = 302 = 900(cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 1200 + 900 = 2100(cm2)
CM
3 tháng 3 2019
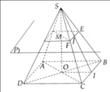
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Diện tích đáy của hình lăng trụ là :
\(\dfrac{{\left( {30 + 40} \right).15}}{2} = 525\left( {c{m^2}} \right)\)
Thể tích của khay là :
\(V = 525.20 = 10500\left( {c{m^3}} \right)\)
14 tháng 7 2023
Gọi số sọt cam và quýt lần lượt là a,b
Theo đề, ta có hệ:
75a+179b=1120 và b-a=2
=>a=3 và b=5
14 tháng 7 2023
Gọi số sọt cam và quýt lần lượt là a,b
Theo đề, ta có hệ:
75a+179b=1120 và b-a=2
=>a=3 và b=5
Diện tích đáy lớn là:
\(S_1=60^2=3600\left(cm^2\right)\)
Diện tích đáy nhỏ là;
\(S_2=30^2=900\left(cm^2\right)\)
Chiều cao là:
\(\sqrt{50^2-\dfrac{30^2}{2}}=5\sqrt{82}\left(cm\right)\)
Thể tích là;
\(V=\dfrac{1}{3}\cdot h\cdot\left(S_1+S_2+\sqrt{S_1\cdot S_2}\right)\)
\(=\dfrac{1}{3}\cdot5\sqrt{82}\left(900+3600+\sqrt{900\cdot3600}\right)\)
\(\simeq95082\left(cm^3\right)\)