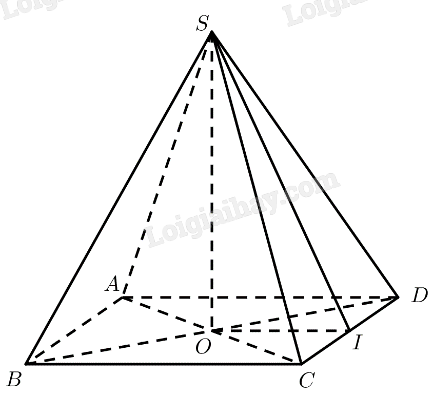
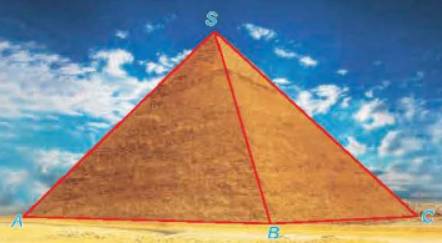
Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) có dạng hình chóp với đây là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m (theo Wikipedia.org).
Giải thích vì sao hình chiếu của đỉnh trên đây là tâm của đáy tháp.







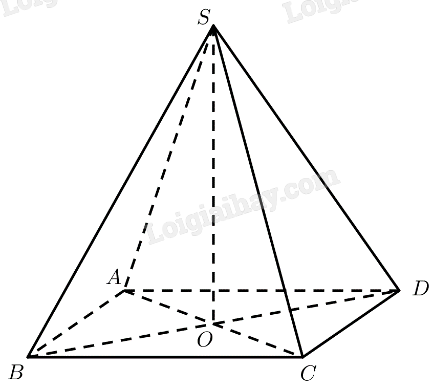
tham khảo:
Tháp lớn tại Bảo tàng Louvre ở Paris có dạng hình chóp với các cạnh bên bằng nhau nên hình chiếu của đỉnh trên đáy tháp sẽ cách đều 4 đỉnh ở đáy mà đáy là hình vuông do đó hình chiếu của đỉnh là tâm của đáy tháp.