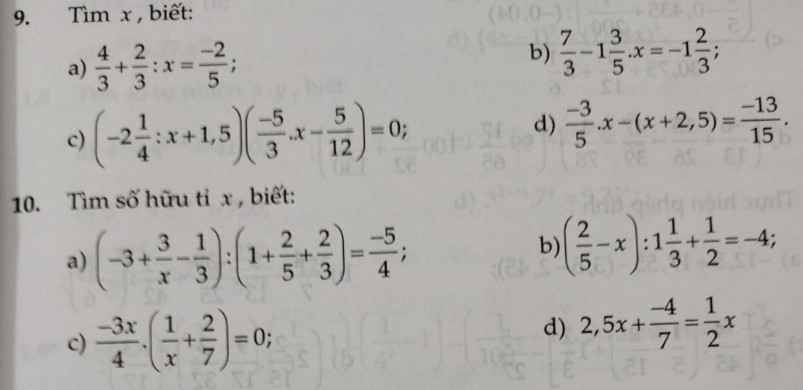 Giúp em với . Em cảm ơn nhiều
Giúp em với . Em cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


71.
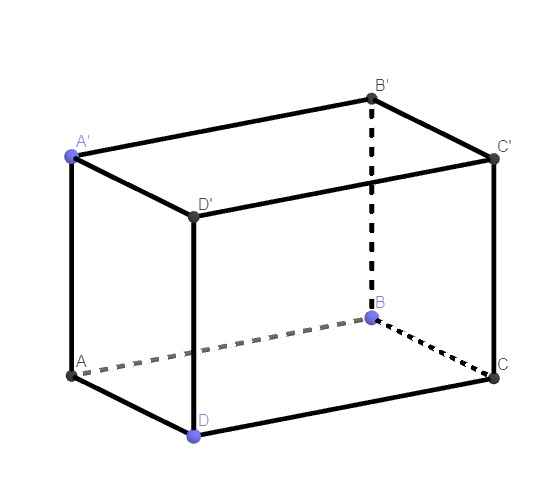
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)





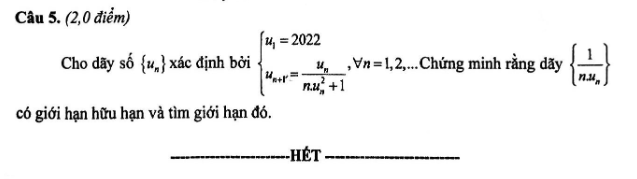
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)


1 are - go
2 don't go
3 is - goes
4 doesn't go
5 is - are
6 is
7 are
8 is - is taking
9 is - works
10 isn't working - is playing
11 do you do - watch
12 are you doing - am watching
13 does Lan do - watches
14 is Lan doing - is watching
15 doesn't work - works
16 does your mother travel
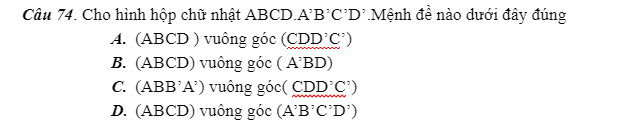
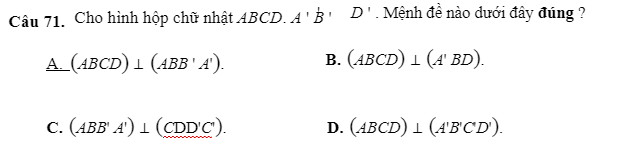







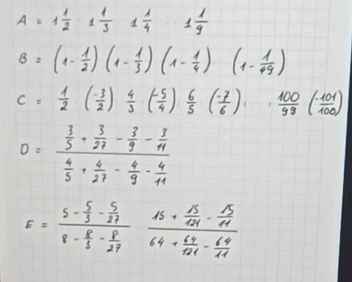
 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ

9. a) \(\dfrac{4}{3}+\dfrac{2}{3}:x=-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{2}{3}:x=-\dfrac{26}{15}\)\(\Rightarrow x=\dfrac{2}{3}:\left(-\dfrac{26}{15}\right)=-\dfrac{5}{13}\)
b) \(\dfrac{7}{3}-1\dfrac{3}{5}.x=-1\dfrac{2}{3}\)
\(\Rightarrow\dfrac{8}{5}x=\dfrac{7}{3}-\left(-\dfrac{5}{3}\right)=\dfrac{7+5}{3}\)
\(\Rightarrow\dfrac{8}{5}x=4\Leftrightarrow x=\dfrac{5}{2}\)
c) \(\left(-2\dfrac{1}{4}:x+1,5\right)\left(\dfrac{-5}{3}.x-\dfrac{5}{12}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-2\dfrac{1}{4}:x=-1.5\\\dfrac{-5}{3}.x=\dfrac{5}{12}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
d) \(-\dfrac{3}{5}.x-\left(x+2,5\right)=-\dfrac{13}{15}\)
\(\Rightarrow-\dfrac{8}{5}.x=-\dfrac{13}{15}+2,5\)
\(\Rightarrow-\dfrac{8}{5}.x=\dfrac{49}{30}\)
\(\Rightarrow x=\dfrac{49}{30}:\left(\dfrac{-8}{5}\right)=-\dfrac{49}{48}\)
10.
a) \(\left(-3+\dfrac{3}{x}-\dfrac{1}{3}\right):\left(1+\dfrac{2}{5}+\dfrac{2}{3}\right)=-\dfrac{5}{4}\)
\(\Rightarrow\left(\dfrac{3}{x}-\dfrac{10}{3}\right):\dfrac{31}{15}=-\dfrac{5}{4}\)
\(\Rightarrow\dfrac{3}{x}-\dfrac{10}{3}=-\dfrac{5}{4}.\dfrac{31}{15}=-\dfrac{31}{12}\)
\(\Rightarrow\dfrac{3}{x}=-\dfrac{31}{12}+\dfrac{10}{3}=\dfrac{3}{4}\)
\(\Leftrightarrow x=4\)
b) \(\left(\dfrac{2}{5}-x\right):1\dfrac{1}{3}+\dfrac{1}{2}=-4\)
\(\Rightarrow\left(\dfrac{2}{5}-x\right):\dfrac{4}{3}=-4-\dfrac{1}{2}=-\dfrac{9}{2}\)
\(\Rightarrow\dfrac{2}{5}-x=-\dfrac{9}{2}.\dfrac{4}{3}=-6\)
\(\Rightarrow x=\dfrac{2}{5}-\left(-6\right)=\dfrac{32}{5}\)
c) \(-\dfrac{3x}{4}.\left(\dfrac{1}{x}+\dfrac{2}{7}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{3x}{4}=0\\\dfrac{1}{x}+\dfrac{2}{7}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\\dfrac{1}{x}=-\dfrac{2}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{7}{2}\end{matrix}\right.\)
d) \(2,5x+\dfrac{-4}{7}=\dfrac{1}{2}x\)
\(\Rightarrow2,5x-\dfrac{1}{2}x=\dfrac{4}{7}\)
\(\Rightarrow2x=\dfrac{4}{7}\Leftrightarrow x=\dfrac{2}{7}\)