cho▲ABC vuông tại A,biếtAB=18cm,AC=24cm 3 đg trung tuyến AM,BN,CP cắt nhau tại G.Tính:AM,GM,GA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3
Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân
CL
19 tháng 7 2017
a, áp dụng định lý pytago đối với tam giá vuông abc tao có mk chỉ làm dc phân a thôi phần b vẫn chưa
BC2 = AB2 + AC2 nghĩ ra bạn ak
BC2= 62 + 82
BC2=36+64
BC2=100
BC=căn bậc 2 của 100 và bằng 10
NT
0
4 tháng 4 2016
mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên
17 tháng 5 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM cũng là phân giác
Xét ΔABG và ΔACG có
AB=AC
\(\widehat{BAG}=\widehat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
b: Xét ΔBIC có
M là trung điểm của BC
MG//IC
Do đó: G là trung điểm của BI
Xét ΔBIC có
M là trung điểm của BC
G là trung điểm của BI
Do đó: MG là đường trung bình
=>MG=1/2CI
17 tháng 9 2023
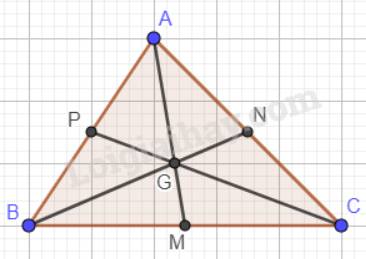
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm)
$AM=\frac{BC}{2}=30:2=15$ (cm) (tính chất đường trung tuyến ứng với cạnh huyền thì bằng 1 nửa cạnh huyền)
$GM=\frac{1}{3}AM=\frac{1}{3}.15=5$ (cm)
$GA=\frac{2}{3}AM=\frac{2}{3}.15=10$ (cm)
Hình vẽ:
