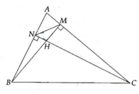
cho tam giác ABC cân tại A . đường cao BM , CN cắt nhau tại H . chứng minh tứ giác BNMC là hinhf thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


I don't now
or no I don't
..................
sorry

Xét tứ giác AMHN có: A M H ^ + A N H ^ = 90 0 + 90 0 = 180 0 => Đpcm
Xét tứ giác BNMC có: B N C ^ = B M C ^ = 90 0 => Đpcm

a: Xét (O) có
ΔABM nội tiếp
AM là đường kính
Do đó: ΔABM vuông tại B
=>BM\(\perp\)AB
mà CH\(\perp\)AB
nên CH//BM
Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
=>AC\(\perp\)CM
mà BH\(\perp\)AC
nên BH//CM
Xét tứ giác BHCM có
BH//CM
BM//CH
Do đó: BHCM là hình bình hành
b:
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AMC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AMC}\)
Ta có: \(\widehat{ABC}+\widehat{BAN}=90^0\)(ΔADB vuông tại D)
\(\widehat{AMC}+\widehat{MAC}=90^0\)(ΔACM vuông tại C)
mà \(\widehat{ABC}=\widehat{AMC}\)
nên \(\widehat{BAN}=\widehat{MAC}\)
Xét (O) có
ΔANM nội tiếp
AM là đường kính
Do đó: ΔANM vuông tại N
=>AN\(\perp\)NM
mà AN\(\perp\)BC
nên BC//NM
Ta có: \(\widehat{CHD}=\widehat{ABC}\)(=90 độ-góc FCB)
\(\widehat{ABC}=\widehat{ANC}\)
Do đó: \(\widehat{CHD}=\widehat{ANC}\)
=>ΔCHN cân tại C
=>CH=CN
mà CH=BM
nên BM=CN
Xét tứ giác BCMN có BC//MN
nên BCMN là hình thang
Hình thang BCMN có BM=CN
nên BCMN là hình thang cân

a: Xét ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)
Do đó: MN//BC
Xét tứ giác BNMC có MN//BC
nên BNMC là hình thang
mà \(\widehat{NBC}=\widehat{MCB}\)
nên BMNC là hình thang cân

a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
Xét tứ giác BNMC có NM//BC
nên BNMC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BNMC là hình thang cân

Vì BM, CN là 2 đường cao ứng vs AC, AB (gt)
\(\Rightarrow\) \(\widehat{AMB}=\widehat{ANC}\) = 90o
\(\Rightarrow\) \(\widehat{AMH}=\widehat{ANH}\) = 90o (H \(\in\) BM; H \(\in\) CN do BM \(\cap\) CN tại H)
Xét tứ giác ANHM có: \(\widehat{AMH}=\widehat{ANH}\)
\(\widehat{AMH}\) và \(\widehat{ANH}\) là 2 góc đối nhau (gt)
\(\Rightarrow\) ANHM là tứ giác nội tiếp (dhnb tứ giác nội tiếp)
Vì BM, CN là 2 đường cao ứng vs AC, AB (gt)
\(\Rightarrow\) \(\widehat{BNC}=\widehat{CMB}\) = 90o
Mà \(\widehat{BNC}\) và \(\widehat{CMB}\) đều nhìn cạnh BC với một góc 90o (cmt)
\(\Rightarrow\) BNMC là tứ giác nột tiếp (dhnb tứ giác nội tiếp)
Chúc bn học tốt!
Gọi O là trung điểm của AH
Ta có: ΔANH vuông tại N(HN⊥AB tại N)
mà NO là đường trung tuyến ứng với cạnh huyền AH(O là trung điểm của AH)
nên \(NO=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔAMH vuông tại M(HM⊥AC tại M)
mà MO là đường trung tuyến ứng với cạnh huyền AH(O là trung điểm của AH)
nên \(MO=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: O là trung điểm của AH(cmt)
nên \(AO=OH=\dfrac{AH}{2}\)(3)
Từ (1), (2) và (3) suy ra OA=ON=OM=OH
⇔A,H,M,N∈(O)
hay tứ giác AMHN nội tiếp đường tròn(O)
Gọi D là trung điểm của BC
Ta có: ΔCBN vuông tại N(CN⊥AB tại N)
mà ND là đường trung tuyến ứng với cạnh huyền BC(D là trung điểm của BC)
nên \(ND=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(4)
Ta có: ΔMBC vuông tại M(MB⊥AC tại M)
mà MD là đường trung tuyến ứng với cạnh huyền BC(D là trung điểm của BC)
nên \(MD=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(5)
Ta có: D là trung điểm của BC(theo cách gọi)
nên \(BD=DC=\dfrac{BC}{2}\)(6)
Từ (4), (5) và (6) suy ra DB=DC=DN=DM
⇔B,C,N,M∈(D)
hay tứ giác BNMC nội tiếp đường tròn(D)(đpcm)

a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
hay BCMN là hình thang