Cho hình lập phương có cạnh bằng a. Tính độ dài đường chéo của hình lập phương đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2023
a) Thể tích hình lập phương là: 4 . 4 . 4 = 64 (cm3)
b) Độ dài cạnh hình lập phương mới là: 4 . 3 = 12 (cm)
Thể tích hình lập phương mới là: 12 . 12 .12 = 1728 (cm3)
c) Thể tích hình lập phương mới gấp số lần thể tích hình lập phương ban đầu là: 1728 : 64 = 27 (lần)
PT
1
CM
8 tháng 10 2017
+ Hình lập phương là hình hộp chữ nhật với a = b = c.
Áp dụng kết quả bài 7b) ta có:
Độ dài đường chéo hình lập phương là:
H9
HT.Phong (9A5)
CTVHS
7 tháng 3 2023
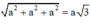
1) Một nữa độ dài đường chéo của hình thôi đã biết: \(\dfrac{24}{2}=12cm\)
Cạnh của hình thôi và một nữa độ dài đường chéo sẽ tạo nên một tam giác vuông tại giao điểm của 2 đường chéo:
Đặt A là một nữa độ dài đường chéo chưa biết.
Áp dụng định lý Pytago ta có:
\(20^2=A^2+12^2\)
\(\Rightarrow A^2=20^2-12^2=256\)
\(\Rightarrow A=\sqrt{256}=16\left(cm\right)\)
Vậy độ dài đường chéo chưa biết là: \(16.2=32\left(cm\right)\)
Diện tích hình thôi là:
\(\dfrac{1}{2}\left(32.24\right)=384\left(cm^2\right)\)
2) Độ dài cạnh của hình lập phương là:
\(\sqrt[3]{125}=5cm\)
Diện tích xung quanh của hình lập phương là:
\(5^2.4=100\left(cm^2\right)\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Thể tích hình lập phương đó là:
V = 33 =27 (cm3)
b) Cạnh của hình lập phương mới là: 2. 3 = 6 (cm)
Thể tích của hình lập phương mới là: V’ = 63 = 216 (cm3)
Thể tích hình lập phương mới gấp số lần thể tích của hình lập phương ban đầu là:
216 : 27=8 (lần)
Chú ý: Khi tăng độ dài cạnh hình lập phương lên a lần thì thể tích hình lập phương tăng lên a3 lần.
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
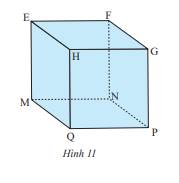
a) Vì hình lập phương có tất cả các cạnh bằng nhau, ta có: EF = FG = GH = HE = EM = HQ = FN = GP = MN = NP = PQ = QM.
Mà MN = 3 cm
Nên EF = NF = 3 cm
b) Các đường chéo của hình lập phương là: EP; FQ; HN; GM
SG
1
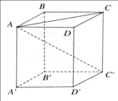
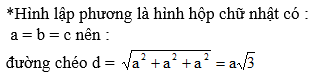
ΔABC vuông tại B
=>\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
ΔA'AC vuông tại A
=>\(A'C=\sqrt{A'A^2+AC^2}=a\sqrt{3}\)
=>Độ dài đường chéo là \(a\sqrt{3}\)