x2 - 2x + m = 0
tìm m để phương trình có 2 nghiệm thỏa mãn x1 - x2 = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TM
1
Những câu hỏi liên quan
MH
19 tháng 3 2023
\(2x^2-\left(4m+3x\right)x+2m^2-1=0\)
\(-x^2-4mx+2m^2-1=0\)
\(\Delta=\left(4m\right)^2+4\left(2m^2-1\right)=24m^2-4\)
Để phương trình có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta>0\Leftrightarrow24m^2-4>0\Leftrightarrow m>\dfrac{1}{\sqrt{6}}\)
Vì phương trình có 2 nghiệm phân biệt, Áp dụng hệ thức Vi ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-4m\\x_1.x_2=1-2m^2\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=6\)
\(\Rightarrow\left(x_1+x_2\right)^2-2\left(x_1.x_2\right)=6\)
\(\Leftrightarrow16m^2-2\left(1-2m^2\right)=6\)
\(\Leftrightarrow20m^2=8\)
\(\Leftrightarrow m^2=\dfrac{2}{5}\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{\dfrac{2}{5}}\left(TM\right)\\m=-\sqrt{\dfrac{2}{5}}\left(\text{Loại vì m}>\dfrac{1}{\sqrt{6}}\right)\end{matrix}\right.\)
Vậy ...
6 tháng 4 2023
a=1; b=-4; c=-m^2+3
Δ=(-4)^2-4*1*(-m^2+3)
=16+4m^2-12=4m^2+4>=4>0
=>Phương trình luôn có hai nghiệm phân biệt
5x1+x2=0 và x1+x2=4
=>4x1=-4 và x1+x2=4
=>x1=-1 và x2=5
x1x2=-m^2+3
=>-m^2+3=-5
=>m^2-3=5
=>m^2=8
=>\(m=\pm2\sqrt{2}\)
YK
1
MH
5 tháng 3 2023
Ta có:
\(\text{∆}'=\left(m+1\right)^2-\left(m^2+m\right)\)
\(=m^2+2m+1-\left(m^2+m\right)=m+1\)
Để phương trình có 2 nghiệm phân biệt x1, x2
\(\Leftrightarrow\text{∆}'>0\Leftrightarrow m+1>0\Leftrightarrow m>-1\)
Áp dụng hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+m\end{matrix}\right.\)
Ta có: \(\dfrac{1}{x_1^2}+\dfrac{1}{x^2_2}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{x_1^2+x^2_2}{x_1^2.x_2^2}=\dfrac{1}{8}\)
\(\Leftrightarrow8[\left(x_1+x_2\right)^2-2x_1.x_2]=x_1^2.x_2^2\)
\(\Leftrightarrow8[[2\left(m+1\right)]^2-2\left(m^2+m\right)]=\left(m^2+m\right)^2\)
\(\Leftrightarrow8\left[4m^2+8m+4-2m^2-2m\right]=m^4+2m^3+m^2\)
\(\Leftrightarrow\)\(8\left[2m^2+6m+4\right]=m^4+2m^3+m^2\)
\(\Leftrightarrow m^4+2m^3-15m^2-48m-32=0\)
\(\Leftrightarrow\left(m+1\right)\left(m^3+m^2-16m-32\right)=0\)
Vì m>-1
\(\Leftrightarrow m^3+m^2-16m-32=0\)
Đến đây nghiêm xấu bạn xem lại đề hoặc có thể sử dụng CTN Cardano
MH
14 tháng 4 2022
Do phương trình có 2 nghiệm x1, x2
\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=5m\\P=x_1.x_2=5m-1\end{matrix}\right.\)
Ta có:
\(x_1^2+x_2^2=2\)
\(\left(x_1^2+2x_1x_2+x_2^2\right)-2x_1x_2=2\)
\(\left(x_1+x_2\right)^2-2x_1x_2-2=0\)
\(\left(5m^2\right)-2\left(5m-1\right)-2=0\)
\(25m^2-10m+2-2=0\)
\(25m^2-10m=0\)
\(5m\left(5m-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{2}{5}\end{matrix}\right.\)
Vậy ...
Y
13 tháng 4 2022
Do pt có 2 nghiệm phân biệt \(x_1,x_2\) nên theo đ/l Vi-ét , ta có :
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=3m\\P=x_1x_2=\dfrac{c}{a}=3m-1\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2=6\)
\(\Leftrightarrow S^2+2P-6=0\)
\(\Leftrightarrow\left(3m\right)^2+2\left(3m-1\right)-6=0\)
\(\Leftrightarrow9m^2+6m-2-6=0\)
\(\Leftrightarrow9m^2+6m-8=0\)
\(\Delta=b^2-4ac=6^2-4.9.\left(-8\right)=324>0\)
\(\Rightarrow\)Pt có 2 nghiệm \(m_1,m_2\)
\(\left\{{}\begin{matrix}m_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-6+18}{18}=\dfrac{2}{3}\\m_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-6-18}{18}=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(m=\dfrac{2}{3};m=-\dfrac{4}{3}\) thì thỏa mãn \(x_1^2+x_2^2=6\)
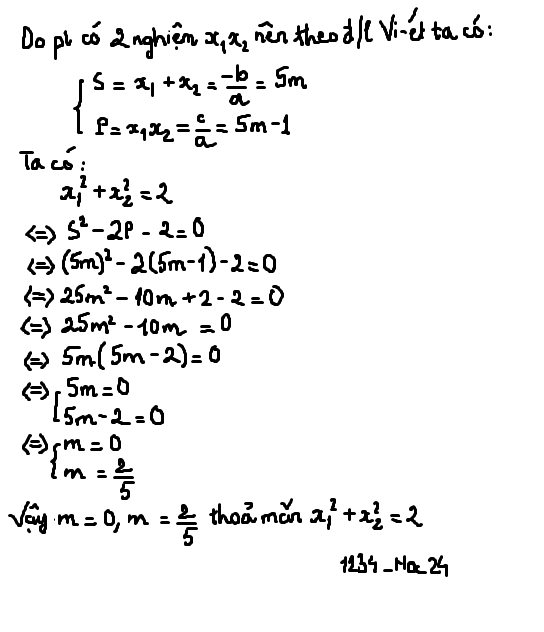
Δ=(-2)^2-4m=4-4m
Để phương trình có 2 nghiệm thì 4-4m>=0
=>4m<=4
=>m<=1
x1-x2=3
=>(x1-x2)^2=9
=>(x1+x2)^2-4x1x2=9
=>2^2-4m=9
=>4m=-5
=>m=-5/4(nhận)