Mng làm nhanh giúp mik vs ah, mik đg cần gấp ah, ai nhanh mik tik nha <3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DM
1
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$
MT
2
KV
2 tháng 5 2023
Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5
HN
1
1 tháng 5 2022
25. amusement.
26. relaxed.
27. diving.
28. operate
29. environmentally
30. largest.
- Bạn tham khảo đáp án nhé! Chúc bạn học tốt.
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
LN
1
XO
27 tháng 7 2020
Gọi số tự nhiên cần tìm là a
Ta có : \(\hept{\begin{cases}a⋮5\\a⋮7\\a⋮9\end{cases}}\Rightarrow a\in BC\left(5;7;9\right)\)
mà a nhỏ nhất có thể
=> \(a=BCNN\left(5;7;9\right)\)
Vì ƯCLN(5;7;9) = 1
=> BCNN(5;7;9) = 5.7.9 = 315
=> a = 315
Vậy số cần tìm là 315
27 tháng 7 2020
Gọi số tự nhiên cần tìm là a
Theo đề bài : a chia hết cho 5 , a chia hết cho 7 , a chia hết cho 9 và a là số tự nhiên nhỏ nhất
=> a = BCNN(5, 7 , 9 )
BCNN(5, 7 , 9) = 5 . 7 . 32 = 315
=> a = 315
Vậy số cần tìm là 315
AH
27 tháng 6 2018
Để M là số nguyên
Thì (x2–5) chia hết cho (x2–2)
==>(x2–2–3) chia hết cho (x2–2)
==>[(x2–2)—3] chia hết cho (x2–2)
Vì (x2–2) chia hết cho (x2–2)
Nên 3 chia hết cho (x2–2)
==> (x2–2)€ Ư(3)
==> (x2–2) €{1;-1;3;-3}
TH1: x2–2=1
x2=1+2
x2=3
==> ko tìm được giá trị của x
TH2: x2–2=-1
x2=-1+2
x2=1
12=1
==>x=1
TH3: x2–2=3
x2=3+2
x2=5
==> không tìm được giá trị của x
TH4: x2–2=-3
x2=-3+2
x2=-1
(-1)2=1
==> x=-1
Vậy x € {1;—1)
S
31 tháng 12 2016
Gọi UCLN(2n + 3,3n + 4) là d
Ta có: 2n + 3 chia hết cho d => 3(2n + 3) chia hết cho d => 6n + 9 chia hết cho d
3n + 4 chia hết cho d => 2(3n + 4) chia hết cho d => 6n + 8 chia hết cho d
=> 6n + 9 - (6n + 8) chia hết cho d
=> 6n + 9 - 6n - 8 chia hết cho d
=> 1 chia hết cho d
=> d = 1
=> UCLN(2n + 3,3n + 4) = 1
31 tháng 12 2016
Gọi d là ƯCLN (2n + 3 ; 3n + 4)
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\3n+4⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(2n+3\right)⋮d\\2\left(3n+4\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}6n+9⋮d\\6n+8⋮d\end{cases}}}\)
\(\Rightarrow6n+9-\left(6n+8\right)⋮d\)
\(6n+9-6n-8⋮d\)
\(1\) \(⋮d\)
\(\Rightarrow d=1\)
Vậy ƯCLN (2n + 3 ; 3n + 4) = 1
TN
1
13 tháng 12 2021
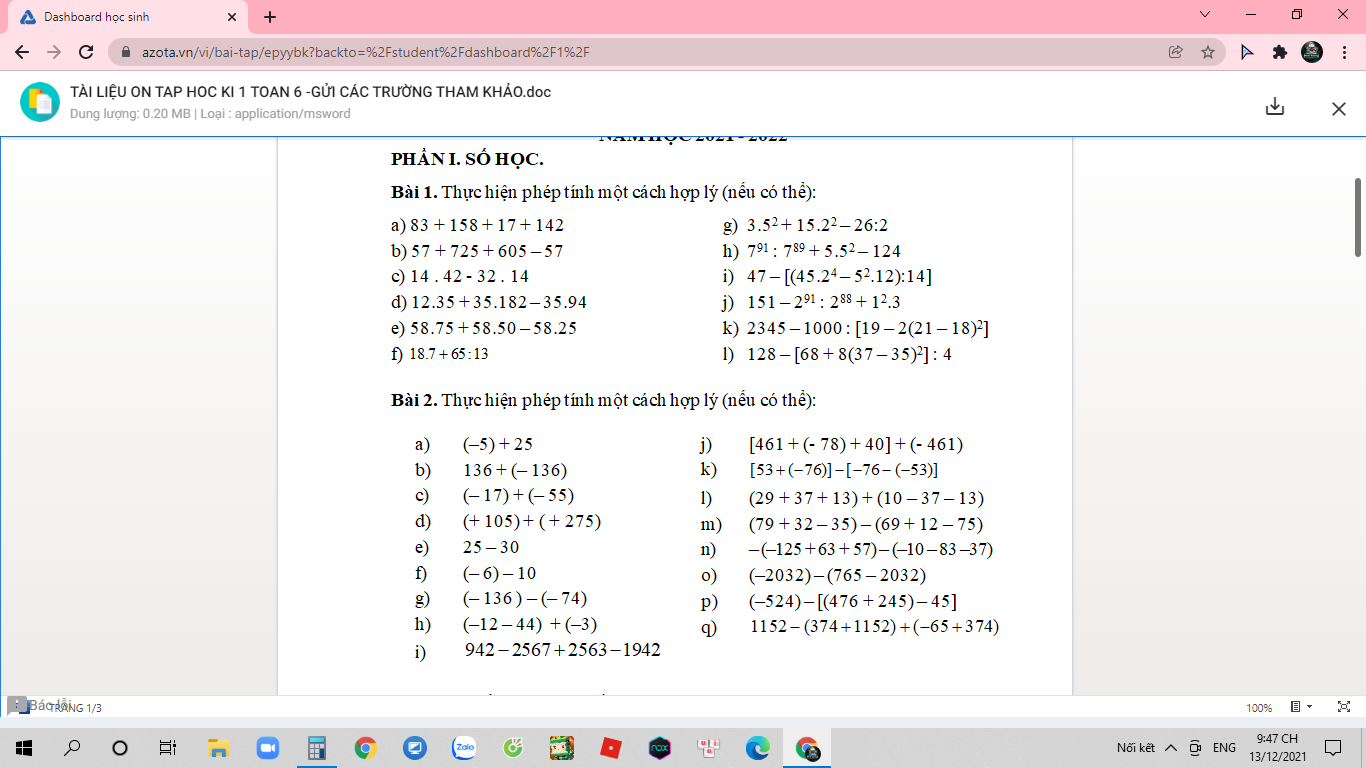
a) \(83+158+17+142.\)
\(=\left(83+17\right)+\left(158+142\right)\) \(=100+300=400.\)
b) \(\text{57 + 725 + 605 - 57}.\)
\(=\left(57-57\right)+\left(725+605\right)\) \(=1330.\)
c) \(14.42-32.14=14.\left(42-32\right)=14.10=140.\)
d) \(12.35+35.182-35.94=35\left(12+182-94\right)=35.100=3500.\)
e) \(58.75+58.50-58.25=58\left(75-25+50\right)=58.100=5800.\)
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$