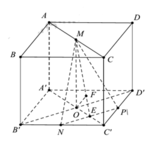
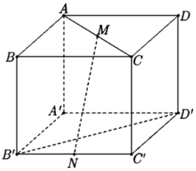
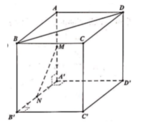
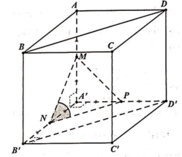
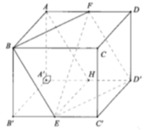
Cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm của AB, B'C'. Góc giữa hai đường thẳng DM và A'N bằng A. 90° B. 60° C. 45° D. 30°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
10 tháng 2 2017
Chọn đáp án C.
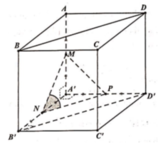
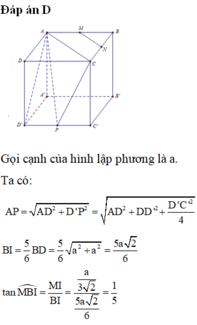
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa ![]()
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên ![]()
Suy ra 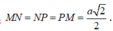
Do đó tam giác MNP đều ![]()
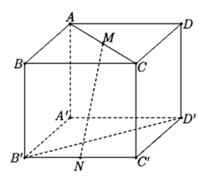


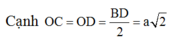
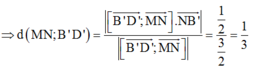




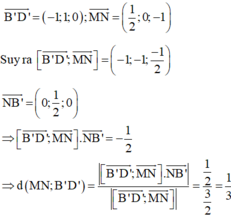


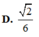

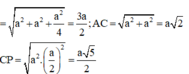
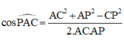
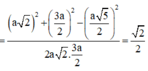
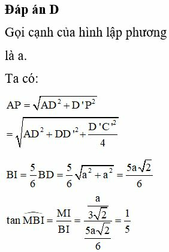

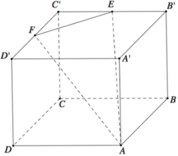
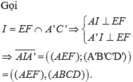
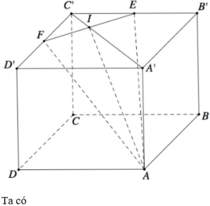

\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
Chọn A