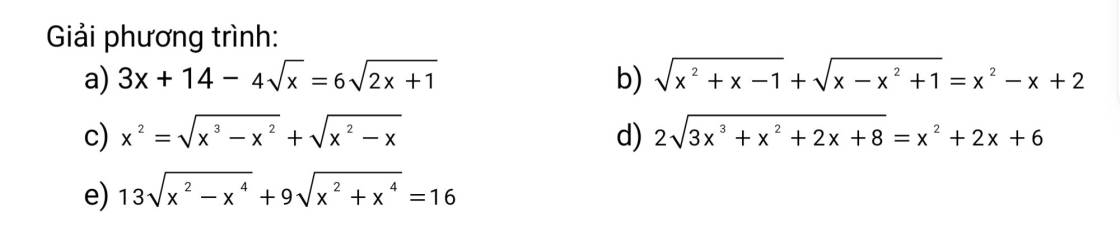 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB

Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)



Tham khảo:
Tầm quan trọng của việc ăn uống đối với sức khỏe của con người:
- Để nuôi sống con người. Nếu không hấp thụ dinh dưỡng từ thức ăn, nước uống con người sẽ chết.
- Để phát triển. Nếu một đứa trẻ không hấp thụ đủ dinh dưỡng cần thiết từ việc ăn uống sẽ dẫn đến thiếu nhiều chất cần thiết cho cơ thể. Hạn chế về phát triển về thể chất cũng như tinh thần, gây một số loại bệnh, hệ miễn dịch kém…

II. Phần tự luận
Câu 1: Động năng của một vật phụu thuộc vào khối lượng và vận tốc
Ví dụ về vật vừa có động năng vừa có thế năng: một chiếc lá đang rơi từ trên cây xuống
Câu 2: Vì nếu cho đá vào trước thì đường và chanh sẽ chậm hòa tan vàotrong nước do nhiệt độ càn cao thì các hạt nguyên tử phân tử chuyển động càng nhanh nên cần hòa tan đường và chanh vào trước để được hòa tan vào trong nước hơn rồi mới nên cho đá vào
II. Phần tự luận:
Câu 3:
Công thực hiện được:
\(A=F.s=180.8=1440J\)
Công suất của người kéo:
\(\text{℘}=\dfrac{A}{t}=\dfrac{1440}{30}==48W\)
Câu 4:
Đổi: \(12km/h=43,2m/s\)
Công suất của ngựa:
\(\text{℘}=\dfrac{A}{t}=\dfrac{F.s}{t}=F.\dfrac{s}{t}=F.\upsilon=320.43,2=13824W\)

\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)








a: \(3x-12-4\sqrt{x}+8=6\sqrt{2x+1}-18\)
=>\(\left(x-4\right)\cdot3-4\left(\sqrt{x}-2\right)=6\left(\sqrt{2x+1}-3\right)\)
=>\(3\left(x-4\right)-\dfrac{4\left(x-4\right)}{\sqrt{x}+2}-6\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(3-\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4
b: \(\Leftrightarrow\sqrt{x^2+x-1}-1+\sqrt{x-x^2+1}-1=x^2-x\)
=>\(\dfrac{x^2+x-1-1}{\sqrt{x^2+x-1}+1}+\dfrac{x-x^2+1-1}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
=>\(\dfrac{\left(x+2\right)\left(x-1\right)}{\sqrt{x^2+x-1}+1}-\dfrac{x\left(x-1\right)}{\sqrt{x-x^2+1}+1}-x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{x+2}{\sqrt{x^2+x-1}+1}-\dfrac{x}{\sqrt{x-x^2+1}+1}-x\right)=0\)
=>x-1=0
=>x=1
c: \(\Leftrightarrow x^2-\sqrt{x^3-x^2}-\sqrt{x^2-x}=0\)
=>\(\sqrt{x}\left(x\sqrt{x}-\sqrt{x^2-x}-\sqrt{x-1}\right)=0\)
=>căn x=0
=>x=0