Quan sát Hình 2.6 và cho biết:
1. Các mặt đáy, mặt bên của các khối đa diện là hình gì?
2. Mỗi khối đa diện có những kích thước nào thể hiện trên hình?

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
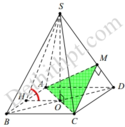
Gọi O là tâm hình vuông ABCD, H là trung điểm AB.
⇒ A B ⊥ S H O ⇒ S A B ; A B C D ^ = S H ; O H ^ = S H O ^ = α . ⇒ c o s α = 1 3 ⇒ tan α = 3 x 2 − 1 = 2 2 ⇒ S O = tan α × O H = a 2 .
Kẻ CM vuông góc với SD M ∈ S D ⇒ m p P ≡ m p A C M .
Mặt phẳng A M C chia khối chóp A.ABCD thành hai khối đa diện gồm M.ACD có thể tích là V 1 và khối đa diện còn lại có thể tích V 2 .
Diện tích tam giác SAB là S Δ S A B = 1 2 . S H . A B = a 2 . 3 a 2 = 3 a 2 4 .
Và
S D = S O 2 + D O 2 = a 10 2 ⇒ S Δ . S C D = 1 2 . S H . S D ⇒ C M = 3 a 10 .
Tam giác MCD vuông tại M ⇒ M D = C D 2 − M C 2 = a 10 ⇒ M D S D = 1 5 .
Ta có:
V M . A C D V S . A C D = M D S D = 1 5 ⇒ V M . A C D = V S . A B C D 10 ⇔ V 1 = V 1 + V 2 10 ⇔ V 1 V 2 = 1 9 .

Chọn đáp án A
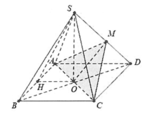
Gọi O là tâm hình vuông ABCD, H là trung điểm của AB
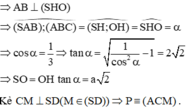
Mặt phẳng (ACM) chia khối chóp S.ABCD thành hai khối đa diện M.ACD có thể tích V1 và khối đa diện còn lại có thể tích V2

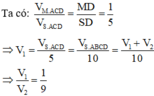

Chọn đáp án D
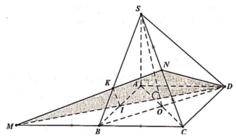
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 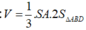
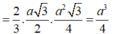
Ta có: N là trung điểm SC nên 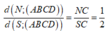
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
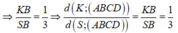
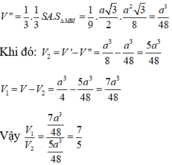

Chọn đáp án D


Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD:

FOR REVIEW |
Tam giác cân có một góc bằng 60 ° thì là tam giác đều. |
Tham khảo
Câu hỏi 1:
- Khối hộp chữ nhật: Mặt đáy mặt bên là các hình chữ nhật.
- Khối lăng trụ tam giác đều: Mặt đáy là hình tam giác, mặt bên là hình chữ nhật.
- Khối chóp tứ giác đều: Mặt đáy là hình vuông, mặt bên là hình tam giác.
Câu hỏi 2:
Mỗi khối đa diện có kích thước chiều dài, chiều rộng của đáy (hoặc cạnh đáy) và chiều cao được thể hiện trên hình.
Phương pháp giải:
Dựa vào hình 2.6 để xác định các mặt đáy, mặt bên của các khối đa diện.
Lời giải chi tiết:
- Khối hộp chữ nhật: Mặt đáy mặt bên là các hình chữ nhật.
- Khối lăng trụ tam giác đều: Mặt đáy là hình tam giác, mặt bên là hình chữ nhật.
- Khối chóp tứ giác đều: Mặt đáy là hình vuông, mặt bên là hình tam giác.