Hình thang vuông ABCD có A = D = 90°, AB = AD =4 cm, DC = 8cm. Tính các góc hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



diện tích hình thang abcd
theo công thức S=1/2h(a+b)
có ab=3cm(ab=1/3CD);Ad=4cm(Ad là chiều cao);DC=9cm
suy ra: S= 1/2 nhân 4(3+9)=24

Đáp án cần chọn là: D
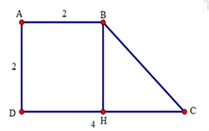
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .

a: Kẻ BH vuông góc CD
Xét tứ giác ABHD có
góc BAD=góc ADH=góc BHD=90 độ
AB=AD
=>ABHD là hình vuông
=>BH=HD=AB=DC/2
=>góc BDH=45 độ
DH=DC/2
=>H là trung điểm của DC
Xét ΔBDC có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBDC cân tại B
=>góc C=45 độ
=>góc ABC=135 độ
c: DC=2*3=6cm
AD=AB=3cm
BC=căn 3^2+3^2=3*căn 2cm
C=6+3+3+3căn 2=12+3căn 2(cm)
Từ B vẽ BH là đường trung trực của DC ( H thuộc DC )
Ta có : .\(\widehat{ADC}\) = \(\widehat{BHC}\)= 90 độ \(\Rightarrow\)ABHD là hình thang cân \(\Rightarrow\)AD = BH = AB = DH = 4 (cm) và DH = HC = 4 (cm) (do BH là đường trung trực)\(\Leftrightarrow\)BHC là tam giác vuông cân \(\widehat{BCH}\)và \(\widehat{HBC}\)= 45 độ
Từ đó : \(\widehat{ABH}\)+ \(\widehat{HBC}\)= \(\widehat{ABC}\) = 90 độ + 45 độ = 135 độ
Vậy các góc của hình thang vuông ABCD là \(\widehat{A}\)=\(\widehat{D}\)= 90 độ ( đề bài cho ) , \(\widehat{ABC}\)= 135 độ và \(\widehat{BCD}\)= 45 độ