phần khoanh tròn ạ baonhieeu tùy tâm :))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2023
c: O là trung điểm của AB
=>OA=OB=R
I là trung điểm của OA
=>OI=OA=0,5R
=>IB=1,5R
ΔIHA đồng dạng với ΔIBM
=>IH/IB=IA/IM
=>IH=3R/8
NA
4 tháng 3 2022
\(f,q\left(x\right)=2x^2-3x-14=0\\ \Leftrightarrow\left(2x^2+4x\right)-\left(7x+14\right)=0\\ \Leftrightarrow2x\left(x+2\right)-7\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\)
\(g,r\left(x\right)=-3x^2+10x-3=0\\ \Leftrightarrow\left(-3x^2+9x\right)+\left(x-3\right)=0\\ \Leftrightarrow-3x\left(x-3\right)+\left(x-3\right)=0\\ \Leftrightarrow\left(-3x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\end{matrix}\right.\)
24 tháng 11 2021
\(c,\) Để PT có 2 nghiệm \(x_1;x_2\Leftrightarrow\Delta=\left(m-4\right)^2+8\left(m-2\right)\ge0\)
\(\Leftrightarrow m^2-8m+16+8m-16\ge0\\ \Leftrightarrow m^2\ge0\left(\text{luôn đúng}\right)\)
Do đó PT có 2 nghiệm với mọi m
\(\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=\dfrac{m-4}{m-2}\left(1\right)\\x_1x_2=\dfrac{2}{2-m}\left(2\right)\end{matrix}\right.\)
Kết hợp \(x_1-x_2=3\text{ với }\left(1\right)\text{ ta được}\)
\(\left\{{}\begin{matrix}x_1=\left(\dfrac{m-4}{m-2}+3\right):2=\dfrac{4m-10}{m-2}\cdot\dfrac{1}{2}=\dfrac{2m-5}{m-2}\\x_2=\dfrac{m-4}{m-2}-\dfrac{2m-5}{m-2}=\dfrac{1-m}{m-2}\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2m-5\right)\left(1-m\right)}{\left(2-m\right)^2}=\dfrac{2}{2-m}\)
\(\Leftrightarrow\left(2m-5\right)\left(1-m\right)=2\left(2-m\right)\\ \Leftrightarrow7m-2m^2-5=4-2m\\ \Leftrightarrow2m^2-9m+9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m=3\text{ và }m=\dfrac{3}{2}\) thỏa đề bài
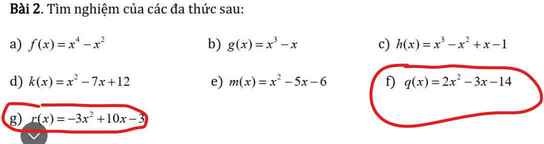
Em chụp ảnh rõ hơn, mỗi câu hỏi chỉ đăng 1 bài, và chỉ đăng nhờ trợ giúp bài chưa làm được thui nha!
1.31:
a: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2
=>AD*AB=AE*AC
b: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC và AC^2=CH*BC
=>AB^2/AC^2=(BH*BC)/(CH*BC)=BH/CH
c: BD/CE
=BH^2/AB:CH^2/AC
\(=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}=\left(\dfrac{BH}{CH}\right)^2\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)
d: BC*BD*CE
\(=BC\cdot\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{AC}\)
\(=\dfrac{BC}{BA\cdot AC}\cdot AH^4=\dfrac{AH^4}{AH}=AH^3\)
e: Đặt HB=x; HC=y(x<y)
AH^2=HB*HC
=>x*y=16
HB+HC=BC
=>x+y=10
xy=16 và x+y=10
=>x,y là các nghiệm của phương trình:
a^2-10a+16=0
=>a=2 hoặc a=8
mà x<y
nên x=2 và y=8
=>BH=2cm; CH=8cm