Bài1: Cho tam giác ABC đều,điểm M nằm trong tam giác ABC,đường thẳng qua M song song với AC cắt BC tại D,đường thẳng qua M song song với BC cắt AB tại E,đường thẳng qua M song song với AB cắt AC tại F . Chứng minh :a,c/m các tứ giác BEMD,AFME,DMFC là các hình thang cân b,độ dài 3 cạnh của tam giác bằng độ dài 3 cạnh của tam giác...
Đọc tiếp
Bài1: Cho tam giác ABC đều,điểm M nằm trong tam giác ABC,đường thẳng qua M song song với AC cắt BC tại D,đường thẳng qua M song song với BC cắt AB tại E,đường thẳng qua M song song với AB cắt AC tại F . Chứng minh :
a,c/m các tứ giác BEMD,AFME,DMFC là các hình thang cân
b,độ dài 3 cạnh của tam giác bằng độ dài 3 cạnh của tam giác nào
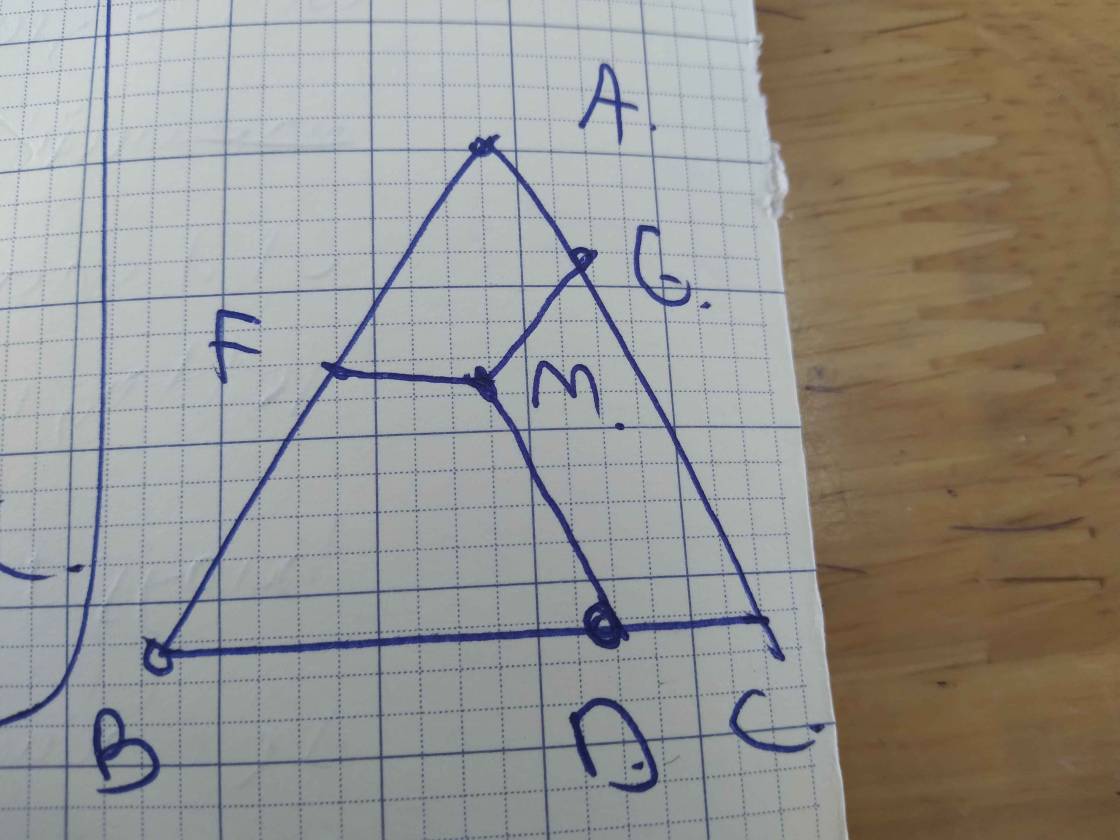
a: MD//AC
=>góc MDB=góc ACB
=>góc MDB=60 độ
Xét tứ giác BEMD có
EM//BD
góc B=góc MDB
=>BEMD là hình thang cân
ME//BC
=>góc AEM=góc ABD=60 độ
Xét tứ giác AEMF có
MF//AE
góc A=góc MEA
=>AEMF là hình thang cân
MF//AE
=>góc CFM=góc CAB=60 độ
Xét tứ giác DCFM có
DM//FC
góc DCF=góc MFC
=>DCFM là hình thang cân
b: Sửa đề: Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của tam giác nào
AEMF là hình thang cân
=>AM=EF
BEMD là hình thang cân
=>BM=ED
FMDC là hình thang cân
=>MC=FD
=>Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của ΔEFD