So sánh : 230 +330+430 và 320+620+820. Mình cần gấp. Tks.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Tính tổng:S=1+52+54+...+5200
=>52S=52+54+56+...+5202
=>25S-S=24S=5202-1
=>S=\(\frac{5^{202}-1}{24}\)
b,So sánh 230+330+430 và 3.2410
3.24^10=3^11.4^15
4^30=4^15.4^15
hiển nhiên 4^15>3^11
=>3.24^10<<4^30<<<2^30+3^20+4^30
Ta có: 230+330+430>230+230+430=231+230.230
=231(1+229) (1)
Lại có:3.24^10=3^11.2^30 (2)
So sánh (1)và (2): Vì 3^11<4^11=2^22<2^29
và 2^30<2^31
=> 3^11.2^30 <(1+2^29)2^31<2^30+3^30+4^30

\(1,\\ \left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\\ \Leftrightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\\left(x-7\right)^{10}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-7=0\\x-7=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=8\end{matrix}\right.\)
\(2,\\ a,\left|2x-3\right|>5\Leftrightarrow\left[{}\begin{matrix}2x-3< -5\\2x-3>5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>4\end{matrix}\right.\\ b,\left|3x-1\right|\le7\Leftrightarrow\left[{}\begin{matrix}3x-1\le7\\1-3x\le7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\le\dfrac{8}{3}\\x\ge-2\end{matrix}\right.\\ c,\cdot x< -\dfrac{3}{2}\\ \Leftrightarrow5-3x+\left(-2x-3\right)=7\Leftrightarrow2-5x=7\Leftrightarrow x=-1\left(ktm\right)\\ \cdot-\dfrac{3}{2}\le x\le\dfrac{5}{3}\\ \Leftrightarrow\left(5-3x\right)+\left(2x+3\right)=7\Leftrightarrow8-x=7\Leftrightarrow x=1\left(tm\right)\\ \cdot x>\dfrac{5}{3}\\ \Leftrightarrow\left(3x-5\right)+\left(2x+3\right)=7\Leftrightarrow5x-2=7\Leftrightarrow x=\dfrac{9}{5}\left(tm\right)\\ \Leftrightarrow S=\left\{1;\dfrac{9}{5}\right\}\)

\(5^{40}=\left(5^4\right)^{10}=625^{10}\)
Mà \(625^{10}>620^{10}\Rightarrow5^{40}>620^{10}\)
Vậy 540 > 62010 ( đpcm )
Ta có :
\(5^{40}=\left(5^4\right)^{10}=625^{10}\)
Vì \(625>620\Rightarrow625^{10}>620^{10}\)
Hay \(5^{40}>620^{10}\)
Vậy \(5^{40}>620^{10}\)
_Chúc bạn học tốt_

Khi nhìn trực tiếp vào phân số ta có thể thấy :
\(\frac{211}{331} < \frac{217}{331} < \frac{217}{330}\)
Vậy \(\frac{211}{331} < \frac{217}{330}\)
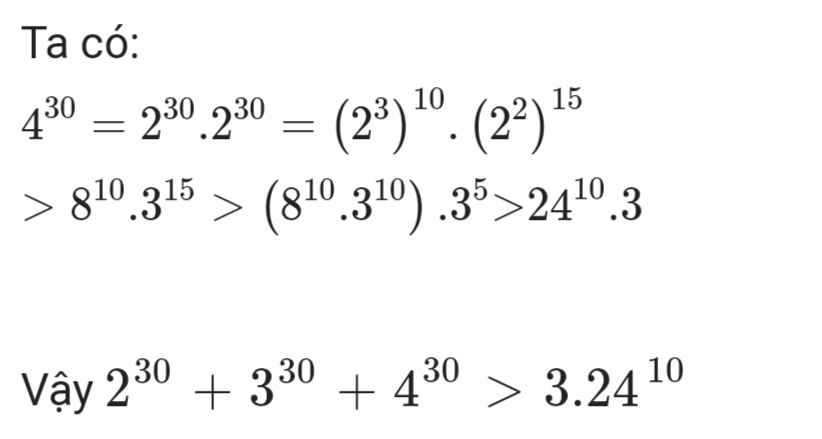
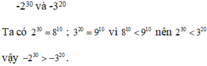
Ta có: \(2^{30}+3^{30}+4^{30}=\left(2^3\right)^{10}+\left(3^3\right)^{10}+\left(4^3\right)^{10}=8^{10}+27^{10}+64^{10}\)
\(3^{20}+6^{20}+8^{20}=\left(3^2\right)^{10}+\left(6^2\right)^{10}+\left(8^2\right)^{10}=9^{10}+36^{10}+64^{10}\)
Vì \(8< 9\)\(\Rightarrow8^{10}< 9^{10}\)
mà \(27< 36\)\(\Rightarrow27^{10}< 36^{10}\)
\(\Rightarrow8^{10}+27^{10}< 9^{10}+36^{10}\)
\(\Rightarrow8^{10}+27^{10}+64^{10}< 9^{10}+36^{10}+64^{10}\)
hay \(2^{30}+3^{30}+4^{30}< 3^{20}+6^{20}+8^{20}\)
so sánh: 2^30 + 3^30 + 4^30 và 3^20 + 6^20 + 8^20
2^30 = ( 2^3)^10 = 8^ 10
3^30 = (3^3)^10 = 27^10
4^30 = (4^3)^10 = 64^10
3^20 = (3^2)^10 = 9^10
6^20 = (6^2) = 36^10
8^20 = (8^2)^10 = 84^10
vì 9^10 > 8^10
36^10 > 27^10
84^10 > 64^10
=> 2^30 + 3^30 + 4^30 < 3^20 + 6^20 + 8^20