Một chất điểm khối lượng 0,01 kg dao động điều hòa một đoạn thẳng dài 4cm với tần số 5Hz. Tại thời điểm t=0 chất điểm đi qua vị trí cân bằng theo chiều dương quỹ đạo. Hợp lực tác dụng vào chất điểm lúc t=0,95 s có độ lớn là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Biên độ dao động của vật:
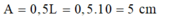
- Tần số góc của dao động:
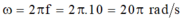
- Gốc thời gian được chọn là lúc vật đi qua vị trí: x = -A/2 = -2,5cm theo chiều dương của trục tọa độ:
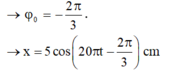

Đáp án A
Biên độ dao động A = MN/2 = 8 cm.
Vật chuyển động nhanh dần khi chuyển động từ biên về VTCB.
Tại t = 0 vật qua vị trí cách O 4 cm và đi nhanh dần theo chiều dương → vật có li độ x = -4 cm theo chiều dương (tức đang ở góc phần tư thứ 3).
→ Pha ban đầu của dao động là -2π/3 rad

Đáp án A
Biên độ dao động A = MN/2 = 8 cm.
Vật chuyển động nhanh dần khi chuyển động từ biên về VTCB.
Tại t = 0 vật qua vị trí cách O 4 cm và đi nhanh dần theo chiều dương → vật có li độ x = -4 cm theo chiều dương (tức đang ở góc phần tư thứ 3).
→ Pha ban đầu của dao động là -2π/3 rad

`A=L/2=10/2=5(cm)`
`\omega =2\pi .f=5\pi(rad//s)`
`a)` Tại `t=0`, vật đi qua VTCB theo chiều dương `=>\varphi =-\pi/2`
`=>` Ptr: `x=5cos(5\pi t-\pi/2)`.
_____
`b)` Tại `t=0`, vật đi qua VTCB theo chiều âm `=>\varphi =\pi/2`
`=>` Ptr: `x=5cos(5\pi t+\pi/2)`
______
`c)` Tại `t=0`, vật qua vị trí có li độ `2,5 cm` theo chiều âm `=>\varphi=\pi/3`
`=>` Ptr: `x=5cos(5\pi+\pi/3)`.
______
`d)` Tại `t=0`, vật qua vị trí có li độ `2,5 cm` theo chiều dương `=>\varphi =-pi/3`
`=>` Ptr: `x=5cos(5\pi -\pi/3)`.

Đáp án A
Khoảng thời gian giữa hai lần liên tiếp qua VTCB
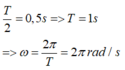
Phương trình dao động của vật có dạng x = 4 cos 2 π t + φ . Lại có:
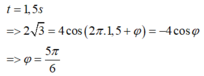

Đáp án A
Khoảng thời gian giữa hai lần liên tiếp qua VTCB 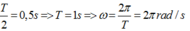
Phương trình dao động của vật có dạng ![]()
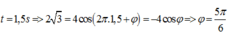

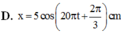

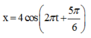
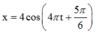
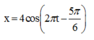
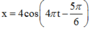
Tham khảo:
Ta có:
\(2A=4\left(cm\right)\Rightarrow A=2\left(cm\right)\)
\(\omega=10\pi\left(rad/s\right)\)
Vậy phương trình:
\(x=2\cdot cos\left(10\pi\cdot t-\dfrac{\pi}{2}\right)\)
Tại \(t=0,95\left(s\right)\) ta có:
\(x=-2\left(cm\right)=0,02\left(m\right)\)
\(\Rightarrow F=-kx=-\omega^2\cdot m\cdot x=-\left(10\pi\right)^2\cdot0,01\cdot-0,02\approx0,197\left(N\right)\)