cho a,b thỏa mãn a/b =3/7 và a+b=7. giá trị biểu thức 5a-3b là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
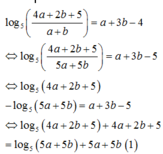
Xét hàm số
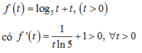
Hàm số f t đồng biến trên 0 ; + ∞
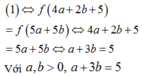
ta có:
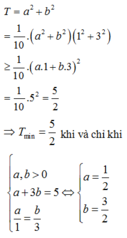
Chọn: D

Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2

Ta đi chứng minh: \(\frac{5b^3-a^3}{ab+3b^3}\le2b-a\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)
Một cách tương tự:\(\frac{5c^3-b^3}{bc+3c^3}\le2c-b;\frac{5a^3-c^3}{ca+3a^2}\le2a-c\)
Cộng lại thì:
\(LHS\le a+b+c=3\)
Đẳng thức xảy ra tại a=b=c=1
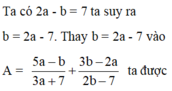
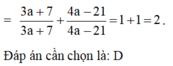
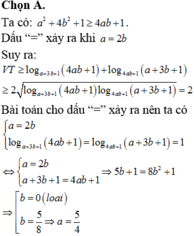
\(\frac{a}{b}=\frac{3}{7}\Rightarrow\frac{a}{3}=\frac{b}{7}=\frac{a+b}{3+7}=\frac{a+b}{10}\)
\(\Rightarrow\frac{a+b}{10}=\frac{7}{10}=0,7\Rightarrow\hept{\begin{cases}a=0,7.3=2,1\\b=0,7.7=4,9\end{cases}}\)
\(\Rightarrow5a-3b=5.2,1-3.4,9=10,5-14,7=-4,2\)
Vậy \(5a-3b=-4,2\)
Bn làm đúng rồi đó