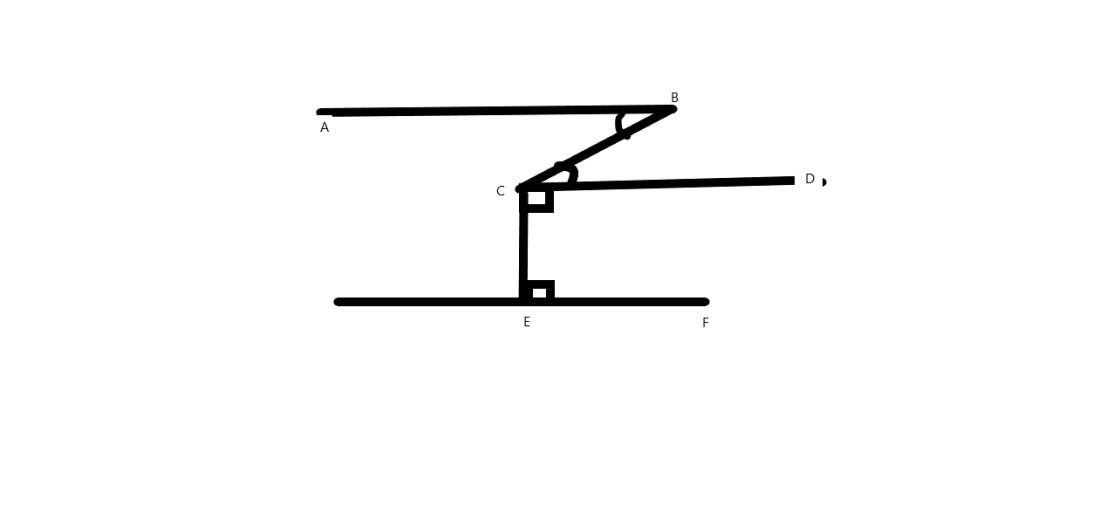
a) chứng minh AB//CD
b) chứng minh AB//EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.Xét tam giác ABM và tam giác CDM có :
AB=CD (gt)
BM=MD(cmt)
BD cạnh chung
=> \(\Delta ABM=\Delta CDM\)
b.*AB//CD
Vì \(\Delta ABM=\Delta CDM\) (cmt )
BAM=MCD( 2 góc tương ứng )
=>AB//CD
*AB=CD
Vì \(\Delta ABM=\Delta CDM\left(cmt\right)\)
=>AB=CD ( 2 cạnh tương ứng )
.Câu d.e.f áp dụng lại như vạy , câu g thì mình lười suy nghĩ ^^

Ta có: AB//CD
nên \(\widehat{ABD}=\widehat{CDB}\) và \(\widehat{ACD}=\widehat{CAB}\)

a) Xét ΔAMD và Δ CMB có :
MA = MC ( M là trung điểm của AC )
Góc AMD = góc CMB ( đối đỉnh )
MB = MD ( gt)
=> ΔAMD = Δ CMB ( c.g.c )
=> AD = BC ( 2 cạnh tương ứng )
*Xét Δv ABM và Δv CDM có :
MB = MD ( gt)
Góc AMB = góc CMD ( đối đỉnh )
=> Δ vABM = Δv CDM ( ch - gn)
=> Góc BAM = góc DCM ( 2 góc tương ứng )
mà góc BAM = 90 độ
=> Góc DCM = 90 độ
a)Xét tam giác ABM và tam giác CBM có:
BM=MD(gt)
góc BMA=góc DMC(đđ)
AM=CM(gt)
Suy ra 2 tam giác này băng nhau(c.g.c)
Suy ra AB=CD(2 cạnh tương ứng)

\(a,\left\{{}\begin{matrix}AE=ED\\BF=FC\end{matrix}\right.\Rightarrow EF\) là đtb hthang ABCD
\(\Rightarrow EF=\dfrac{AB+CD}{2};EF//AB//CD\left(đpcm\right)\)
\(b,\left\{{}\begin{matrix}BF=FC\\FK//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow AK=KC\) hay BK là trung tuyến tg ABC
\(c,\left\{{}\begin{matrix}AE=ED\\EI//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow BI=ID\Rightarrow IE\) là đtb tg ABD
\(\Rightarrow IE=\dfrac{1}{2}AB.hay.AB=2IE\)
\(d,\left\{{}\begin{matrix}BF=FC\\AK=KC\end{matrix}\right.\Rightarrow FK\) là đtb tg ABC
\(\Rightarrow FK=\dfrac{1}{2}AB=IE\left(đpcm\right)\)
\(e,\) Ta có \(FK=IE=\dfrac{AB}{2}=3\)
\(KF=EF-EI-FK=\dfrac{AB+CD}{2}-3-3=8-3-3=2\)
a) Ta có:
\(\widehat{ABC}=\widehat{BCD}\) (gt)
Nên hai góc này so le trong
⇒ AB//CD
b) Ta có:
\(\widehat{DCE}=\widehat{CEF}=90^o\) (gt)
⇒ EF//CD
Mà: AB//CD
⇒ AB//EF
có :
`góc ABC = góc BCD`
Mà 2 góc này ở vị trí solo trong
`=>AB` // `CD`
có :
\(DC\perp CE\)
\(EF\perp CE\) `=> DC` // `EF`
lại có :AB//CD
CD//EF = > AB//EF