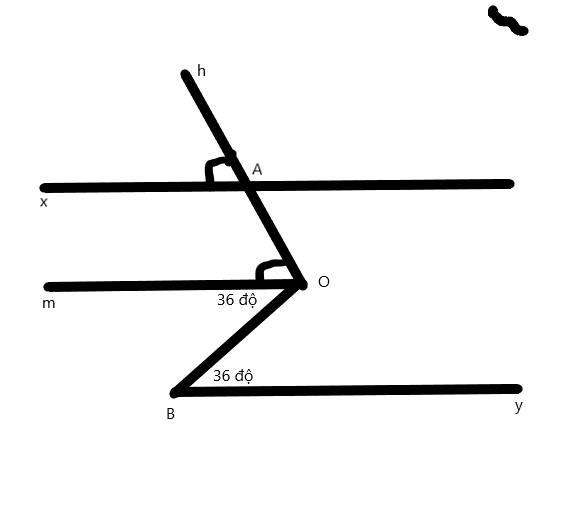
a) chứng minh Ax//Om
b) chứng minh Ax//By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 3 2022
a: Xét ΔAMC và ΔOMB có
AM=OM
\(\widehat{AMC}=\widehat{OMB}\)
MC=MB
Do đó:ΔAMC=ΔOMB
b: Xét tứ giác ABOC có
M là trung điểm của AO
M là trung điểm của BC
Do đó: ABOC là hình bình hành
Suy ra: AC//BO
c: Hình bình hành ABOC có AB=AC
nên ABOC là hình thoi
=>CO=CA
24 tháng 10 2021
a) ta có: \(\widehat{BAx}+\widehat{ABy}=60^o+120^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒Ax//By
b) ta có: \(\widehat{CBy}+\widehat{BCz}=140^o+40^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒By//Cz
c) Ax//By, By//Cz⇒Ax//Cz
TL
24 tháng 10 2021
cảm ơn bạn nhiều lắm ko bt bạn sinh năm bao nhiêu để dễ xưng hô
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
1 tháng 11 2021
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MQ là tiếp tuyến có Q là tiếp điểm
Do đó: MA=MQ
Xét (O) có
EQ là tiếp tuyến có Q là tiếp điểm
EB là tiếp tuyến có B là tiếp điểm
Do đó: EQ=EB
Ta có: QM+QE=EM
hay EM=AM+BE
LD
1
B
24 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
PT
1
CM
15 tháng 6 2018
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
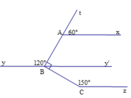
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
a: góc hAx=góc mOA
mà hai góc này đồng vị
nên Ax//Om
b: góc mOA=góc yBO
mà hai góc này so le trong
nên Om//By
mà Ax//Om
nên Ax//By
a) Ta có:
\(\widehat{xAh}=\widehat{mOA}\) (gt) nên hai góc này là hai góc đồng vị
⇒ Ax//Om
b) Ta có:
\(\widehat{OBy}=\widehat{mOB}=36^o\) nên hai góc này là hai góc so le trong
⇒ By//Om
Mà: Ax//Om (cmt)
⇒ Ax//By