CM định lý :"Hai tia phân giác cảu hai góc kề bù thì vuông góc với nhau "
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo nhé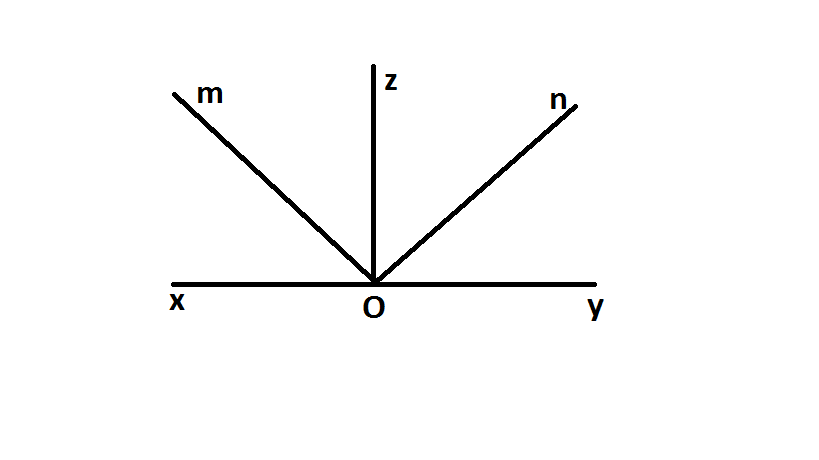
Ta có góc \(\widehat{\text{xOz}}\) + \(\widehat{\text{zOy}}\) = 180\(^o\)(kề bù)
=> 2(\(\widehat{mOz}\) +\(\widehat{zOn}\)) = 180\(^o\)
=> \(\widehat{mOz}\) + \(\widehat{zOn}\) = 90\(^o\)
=>\(\widehat{mOn}\) = 90\(^o\) (vì \(\widehat{xOz}\), \(\widehat{xOz}\) kề nhau)
=> Tia Om vuông góc tia On
Vậy 2 tia phân giác của 1 cặp góc kề bù thì vuông góc với nhau

Câu 9: Khẳng định nào sau đây
A . Hai góc bằng nhau là hai góc đối đỉnh.
B. Đường trung trực của đoạn thẳng thì đi qua trung điểm của đoạn thẳng ấy.
C. Hai đường thẳng không cắt nhau thì song song.
D. Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng đó.
.Câu 10: Trong các phát biểu sau đây thì phát biểu nào đúng?
A. Hai tia phân giác của cặp góc bù nhau thì vuông góc với nhau.
B. Hai tia phân giác của cặp góc kề nhau thì vuông góc với nhau.
C. Hai tia phân giác của cặp góc đối đỉnh thì vuông góc với nhau.
D. Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau.
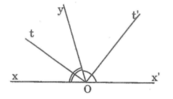

Giả sử ta có hai góc cạnh bù AOB và BOC. Ta cần chứng minh rằng hai tia phân giác AO và CO vuông góc với nhau.
Để chứng minh điều này, chúng ta sẽ sử dụng một số bước sau:
Bước 1: Vẽ tia phân giác OD của góc AOB và tia phân giác OE của góc BOC.
Bước 2: Ta cần chứng minh rằng góc AOD và góc COE là như nhau. Điều này có thể được chứng minh bằng cách sử dụng định lý góc phân giác, tức là góc AOD chia đôi góc AOB và góc COE chia đôi góc BOC.
Bước 3: Ta cần chứng minh rằng góc AOD và góc COE là hai góc vuông góc với nhau. Điều này có thể được chứng minh bằng cách sử dụng định lý góc phân giác của góc cạnh, tức là nếu một tia phân giác của một góc góc với tia phân giác của góc cạnh thì hai tia phân giác đó cũng góc với góc nhau.
Vì vậy, ta đã chứng minh được rằng hai tia phân giác AO và CO vuông góc với nhau khi hai góc kề bù AOB và BOC.
...