Vẽ 5 điểm A;B;C;D;E thỏa mãn các điều kiện sau:
+ C giữa A và B.
+ A;B và E thẳng hàng.
+ A và B cùng phía đối với E.
+ Điểm D thuộc đường thẳng BC.
Kể tên các điểm khác phía đối với B
nhanh thì mình tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 3 2017
a) Chọn một điểm trong năm điểm đã cho thì ta nối điểm đó với 4 điểm còn lại tạo thành 4 đường thẳng. Làm như vậy với tất cả 5 điểm ta được 4.5 = 20 đường thẳng. Khi đó, mỗi đường thẳng được tính 2 lần (ví dụ đường thẳng AB và đường thẳng BA chỉ là một). Do đó, số đường thẳng thực tế là 20:2 = 10.
b) Lập luận tương tự ý a), thay số 5 bằng n. Ta có số đường thẳng là n ( n − 1 ) 2
HT
19 tháng 9 2015
a, Trong 5 điểm không có 3 điểm nào thẳng hàng
=> Số đường thẳng tạo được là:
5.(5 - 1) : 2 = 10 (đường thẳng)
b, - Trong 3 điểm vẽ được: 3.(3 - 1) : 2 = 3 (đường thẳng)
- Trong 3 điểm thẳng hàng vẽ được 1 đường thẳng
=> Số đường thẳng bị hụt đi là:
3 - 1 = 2 (đường thẳng)
=> Trong 5 điểm trong đó có đúng 3 điểm thẳng hàng thì tạo được số đường thẳng là:
10 - 2 = 8 (đường thẳng)
ĐS: a, 10 đường thẳng
b, 8 đường thẳng
15 tháng 9 2017
Đỗ Đức Đạt
Đáp án đúng là a, vì
Số tất cả đường thẳng đi qua 2 trong 5 điểm là:
\(5.4:2=10\)
Đáp số: 10
21 tháng 2 2020
Ta có:
a.(a−1)2a.(a−1)2 −1=20−1=20
a.(a−1)2=20+1a.(a−1)2=20+1
a.(a−1)2=21a.(a−1)2=21
a.(a−1)=21.2a.(a−1)=21.2
=42=7.6=42=7.6
Vậy a=7
k cho minh nha
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
a, Với 5 điểm không thẳng và trong đó bất cứ 3 điểm nào cũng không thẳng hàng với nhau thì làm như sau em nhé.
Cứ 1 điểm sẽ tạo với ( 5 - 1) điểm còn lại ( 5 - 1) đường thẳng
Có 5 điểm tạo được số đường thẳng là: ( 5-1) \(\times\) 5
Theo cách tính trên mỗi đường thẳng được tính hai lần nên số đường thẳng được tạo là: ( 5 - 1) \(\times\) 5: 2 = 10 ( đường thẳng)
b, Với n điểm không thẳng hàng và trong đó bất cứ 3 điểm nào cũng không thẳng hàng với nhau thì làm như sau:
Cứ 1 điểm tạo với n - 1 điểm còn lại n - 1 đường thẳng
Với n điểm sẽ tạo được số đường thẳng là: (n-1) \(\times\) n
Theo cách tính trên mỗi đường thẳng sẽ được tính 2 lần nên số đường được tạo là:
( n- 1)n : 2 ( đường thẳng)
CM
9 tháng 7 2017
a) Trên tia Ox có OA < OB nên điểm A nằm giữa hai điểm O và B.
b) Chú ý: trên tia Ox có OA < OC < OB nên điểm C nằm giữa hai điểm A và B.
HN
18 tháng 3 2022
a) Vẽ được 10 đường thẳng. Các đường thẳng đó là AB, AC, AD, AE, BC, BD, BE, CD, CE, DE.
b) Vẽ được \(\dfrac{n\left(n-1\right)}{2}\) đường thẳng.
c) \(\dfrac{n\left(n-1\right)}{2}\)=28 \(\Rightarrow\) n=8.
Vậy có 8 điểm phân biệt cho trước thỏa yêu cầu đề bài.
22 tháng 8 2016
Vì 2 dường thẳng d và d' có hai góc trong cùng phía bù nhau nên chúng song song với nhau
Do đó hai đường thẳng d và d' không cắt nhau.
CM
7 tháng 10 2018
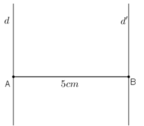
Giả sử đường thẳng d và d’ cắt nhau tại O.
Khi đó qua điểm O ta vẽ được hai đường thẳng phân biệt (d và d’) cùng vuông góc với đường thẳng a (Vô lý).
Vậy đường thẳng d và d’ không cắt nhau.