cho đường tròn đường kính AB ,điểm C nằm trên (C) (CA<CB) tiếp tuyến với đường tròn tại B và C cắt tại D.Từ C hạ đường vuông góc với BD tại Ha.DO cắt CH,CB tại M,N .a) CNHD nội tiếp .b) CM=CO.c) AB=CD tại E CM: EA=EB=EC^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các bán kính của đường tròn là: OA, OB, OC.
Các dây của đường tròn là: CA,CB.

Các bán kính của đường tròn là: OA, OB, OC.
Các dây của đường tròn là: CA,CB.

xét đường tròn tâm o có
C là điểm chính giữa nằm trên nửa đường tròn
=> cung CA = cung CB
=> CA=CB điều 1 ...liên hệ giữa cung và dây
mặt khác. góc CBNlaf góc nội tiếp chắn cung CN
góc NMC là góc nội tiếp chắn cung CN
=> góc CBN = góc NMC
lại có cung BN = cung CM
=> BN=MC
xét tam giác CBN và Tam giác NMC có
CN chung
BN = MC
góc CBN= góc NMC
=> 2 tam giác bằng nhau => MN = BC điều 2
từ 1 và 2 => MN= CA =CB

bạn tham khảo ở đây nha,mình từng giải rồi
https://hoc24.vn/cau-hoi/cho-duong-tron-o-duong-kinh-ab-tren-tiep-tuyen-tai-a-cua-duong-trong-o-lay-diem-c-ve-tuyep-tuyen-cn-va-cat-tuyen-cde-tia-cd-nam-giua-2-tai-ca-co-de-thuoc-duong-tron-o-d-nam-giua-c-va-e.1081799079177

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
=>BC\(\perp\)AC tại C
=>BC\(\perp\)AE tại C
=>ΔCEF vuông tại C
Xét (O) có
\(\widehat{ICB}\) là góc tạo bởi tiếp tuyến CI và dây cung CB
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
Do đó: \(\widehat{ICB}=\widehat{CAB}\)
mà \(\widehat{CAB}=\widehat{BFD}\left(=90^0-\widehat{CBA}\right)\)
nên \(\widehat{ICB}=\widehat{BFD}\)
mà \(\widehat{BFD}=\widehat{IFC}\)(hai góc đối đỉnh)
nên \(\widehat{ICB}=\widehat{IFC}\)
=>\(\widehat{ICF}=\widehat{IFC}\)
=>IC=IF
Ta có: \(\widehat{ICF}+\widehat{ICE}=\widehat{ECF}=90^0\)
\(\widehat{IFC}+\widehat{IEC}=90^0\)(ΔECF vuông tại C)
mà \(\widehat{ICF}=\widehat{IFC}\)
nên \(\widehat{ICE}=\widehat{IEC}\)
=>IC=IE
mà IC=IF
nên IE=IF
=>I là trung điểm của EF
b: Vì ΔCEF vuông tại C
nên ΔCEF nội tiếp đường tròn đường kính EF
=>ΔCEF nội tiếp (I)
Xét (I) có
IC là bán kính
OC\(\perp\)CI tại C
Do đó: OC là tiếp tuyến của (I)

Nguyễn Lê Phước Thịnh
Akai Haruma
Nguyễn Việt Lâm
Hồng Phúc
Giúp em câu c là đc ạ

Chọn đáp án A.
Ta có:
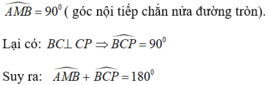
Do đó, tứ giác PMAC là tứ giác nội tiếp
a: Xét (O) có
DC,DB là tiếp tuyến
=>DC=DB
mà OB=OC
nên OD là trung trực của BC
=>OD vuông góc BC tại N
góc DNC=góc DHC=90 độ
=>DHNC nội tiếp
b: Xét ΔDCB có
DN,Ch là đường cao
DN cắt CH tại M
=>M là trực tâm
=>BM vuông góc CD
=>BM//CO
Xét tứ giác OBMC có
OB//MC
MB//OC
OB=OC
=>OBMC là hình thoi
=>CM=CO