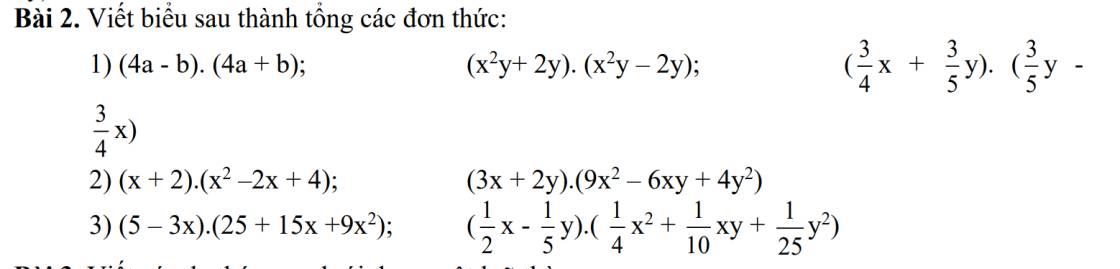 mong Akai Haruma;cô nguyễn thị thương hoài và mn giúp đỡ ạ
mong Akai Haruma;cô nguyễn thị thương hoài và mn giúp đỡ ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 2x2 + 5y2 - 2xy + 2x + 2y
A = x2 - 2xy + y2 - 2x - 2y + 1 + x2 + 4x + 4 + 4y2 + 4y + 1 - 6
A = ( x - y)2 - 2( x + y) + 1 + ( x + 2)2 + ( 2y + 1)2 - 6
A = ( x - y - 1)2 + ( x + 2)2 + ( 2y + 1)2 - 6
Do : ( x - y - 1)2 ≥ 0 ∀x
( x + 2)2 ≥ 0 ∀x
( 2y + 1)2 ≥ 0 ∀x
⇒ ( x - y - 1)2 + ( x + 2)2 + ( 2y + 1)2 ≥ 0
⇒ ( x - y - 1)2 + ( x + 2)2 + ( 2y + 1)2 - 6 ≥ -6
⇒ AMIN = - 6
Ah , sorry bạn nha , mk làm nhầm rùi
A = 2x2 + 5y2 - 2xy + 2x + 2y
A = x2 - 4xy + 4y2 + x2 + 2xy + y2 + 2x + 2y + 1 - 1
A = ( x - 2y)2 + ( x + y)2 + 2( x + y) + 1 - 1
A = ( x - 2y)2 + ( x + y + 1)2 - 1
Do : ( x - 2y)2 ≥ 0 ∀x
( x + y + 1)2 ≥ 0 ∀x
⇒ ( x - 2y)2 + ( x + y + 1)2 ≥ 0
⇒ ( x - 2y)2 + ( x + y + 1)2 - 1 ≥ - 1
⇒ AMIN = -1 ⇔ x = \(\dfrac{-1}{3};y=\dfrac{-2}{3}\)


Ta có :
\(997^2=\left(1000-3\right)^2=1000^2-2.3.1000+3^2=1000000-6000+9=994009\)
Wish you study well !!!

Lời giải:
Từ điều kiện đã cho của $a,b,c$, tồn tại $x,y,z>0$ sao cho:
\((a,b,c)=\left(\frac{x}{\sqrt{(x+y)(x+z)}}; \frac{y}{\sqrt{(y+z)(y+x)}}; \frac{z}{\sqrt{(z+x)(z+y)}}\right)\)
Khi đó, áp dụng BĐT Cauchy ta có:
\(M=a+b+c=\frac{x}{\sqrt{(x+y)(x+z)}}+\frac{y}{\sqrt{(y+z)(y+x)}}+\frac{z}{\sqrt{(z+x)(z+y)}}\)
\(\leq \frac{1}{2}\left(\frac{x}{x+y}+\frac{x}{x+z}\right)+\frac{1}{2}\left(\frac{y}{y+z}+\frac{y}{y+x}\right)+\frac{1}{2}\left(\frac{z}{z+x}+\frac{z}{z+y}\right)\)
hay \(M\leq \frac{1}{2}\left(\frac{x+y}{x+y}+\frac{y+z}{y+z}+\frac{z+x}{z+x}\right)=\frac{3}{2}\)
Vậy \(M_{\max}=\frac{3}{2}\Leftrightarrow x=y=z\Leftrightarrow a=b=c=\frac{1}{2}\)
Cách khác:
Ta có:
\(a^2+b^2+c^2+2abc=1\)
\(\Leftrightarrow (a+b+c)^2-2(ab+bc+ac)+2abc=1\)
\(\Leftrightarrow (a+b+c)^2-2(a+b+c)+1=2+2(ab+bc+ac)-2(a+b+c)-2abc\)
\(\Leftrightarrow (a+b+c)^2-2(a+b+c)+1=2[1-(a+b+c)+(ab+bc+ac)-abc]\)
\(\Leftrightarrow (a+b+c)^2-2(a+b+c)+1=2(1-a)(1-b)(1-c)\) (đây là đẳng thức khá quen thuộc)
Áp dụng BĐT Cauchy ngược dấu:
\((a+b+c)^2-2(a+b+c)+1=2(1-a)(1-b)(1-c)\leq 2\left(\frac{1-a+1-b+1-c}{3}\right)^3=\frac{2[3-(a+b+c)]^3}{27}\)
\(\Leftrightarrow t^2-2t+1\leq \frac{2(3-t)^3}{27}\) (đặt \(a+b+c=t\))
\(\Leftrightarrow 2t^3+9t^2-27\leq 0\)
\(\Leftrightarrow (2t-3)(t+3)^2\leq 0\Rightarrow 2t-3\leq 0\Rightarrow t=M=a+b+c\leq \frac{3}{2}\)
Vậy \(M_{\max}=\frac{3}{2}\Leftrightarrow a=b=c=\frac{1}{2}\)

(6x+5)^2.(3x+2).(x+1)=35
<=>(36x^2+60x+25)(3x^2+5x+2)=35
t=3x^2+5x+2
=>(12t+1)t=35
=>12t^2+t-35=0 =>giải ptb2 tìm t sau đó thay vào giải tiếp ptb2 tìm x



Bài 1 : (4a - b).(4a + b) = 16a2 + (-b2)
(\(x^2y\) + 2y)(\(x^2\)y - 2y = \(x^4\).y2 + (- 4y2)
(\(\dfrac{3}{4}\)\(x\) + \(\dfrac{3}{5}\)y)(\(\dfrac{3}{5}\)y - \(\dfrac{3}{4}\)\(x\)) = \(\dfrac{9}{25}\)y2 + (- \(\dfrac{9}{16}\)\(x^2\))
2; (\(x+2\))(\(x^2\) - 2\(x\) + 4) = \(x^3\) + 8
(3\(x\) + 2y)(9\(x^2\) - 6\(xy\) + 4y2) = 27\(x^3\) + 8y3
3, (5- 3\(x\))(25 + 15\(x\) + 9\(x^2\)) = 125 + ( -27\(x^3\))
(\(\dfrac{1}{2}\)\(x\) - \(\dfrac{1}{5}\)y).(\(\dfrac{1}{4}\)\(x^2\) + \(\dfrac{1}{10}\)\(xy\) + \(\dfrac{1}{25}\)y2 = \(\dfrac{1}{8}\)\(x^3\) + (-\(\dfrac{1}{125}\)y3)
em cảm ơn cô ạ