x. y* 99=xx. yy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1980=3.5.131 là tích 3 số nguyên tố
vì x, y là chữ số nên chỉ có thể
x=3, y=5 => xx=33, yy=55 hoặc ngược lại vai trò x,y
=> (33+55).3.5=1320 không bằng 1980
vậy không tồn tại x,y thỏa bài toán

Biến đổi đẳng thức đã cho về dạng:
(x+y)xy=180
Từ đây suy ra x=4, y=5 hoặc x=5, y=4

1980=3.5.131 là tích 3 số nguyên tố
vì x, y là chữ số nên chỉ có thể
x=3, y=5 => xx=33, yy=55 hoặc ngược lại vai trò x,y
=> (33+55).3.5=1320 không bằng 1980
vậy không tồn tại x,y thỏa bài toán
(xx+yy).x.y=1980
=(10.x+x+10.y+y).x.y=1980
=(11.x+11.y).x.y=1980
=11.(x+y).x.y=1980
=(x+y).x.y=1980:11
=(x+y).x.y=180
180=22.32.5
180=4.9.5
TH1:x=4,y=9
=>(44+99).4.9=5148(loại)
TH2:x=9,y=5
=>(99+55).9.5=6930(loại)
TH3:x=5,y=4
=>(55+44).5.4=1980(thoả mãn đề bài)
Vậy x=5,y=4 hoặc x=4,y=5

a)khi x=8 thì y=15
=> 8.15=120
Vậy hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ là 120.
b) biểu diễn x theo y:
y=a/c=> y=120/8=>a=8.15
c) khi x =6
=>y=120/6
=>y=20
Khi x=10
=>y=120:10
=>y=12.

(10).(x,y).(10).(9,9)=100.(xx,yy)
(xy).(99)=(xxyy)
(10x+y).(99)=1000x+100x+10y+y
99x+99y=1100+11y
88y=110x
(88:22).y=(110:22)x
4. y=5 .x <=> y=5 ; x=4
Tìm các chữ số x,y sao cho: xxyy=xx*xx+yy*yy (x,y khác 0)
Các bạn giải chi tiết giúp mình, mình tick


\(A=xx+yy=x^2+y^2\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(1\cdot x+1\cdot y\right)^2=4\)
\(\Rightarrow2\left(x^2+y^2\right)\ge4\)
\(\Rightarrow A\ge2\)
Dấu "=" xảy ra khi \(\left\{\begin{matrix}x+y=2\\x=y\end{matrix}\right.\)\(\Rightarrow x=y=1\)
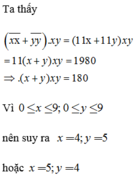
(10).(X,Y).(10).(9,9)=100.(XX,YY)
(XY).(99)=(XXYY)
(10X+Y).(99)=1000X+100X+10Y+Y
990X+99Y=1100X+11Y
88Y=110X
(88:22).Y=(110:22)X
4. Y=5 .X <=>
Y=5 ; X=4
thử lại
4,5 x 9,9 = 44,55
Sai đầu bài rồi bạn! ơi! không thể nào x.y x 99 lại ra một số thập phân có 2 chữ số ở phần thập phân đâu!