13. Cho tam giác ABC, điểm M trên cạnh BC. Vẽ ME // AB( E ϵ AC); MF // AC( F ϵ AB). Xác định vị trí của điểm M để tia MA là tia phân giác của góc EMF.
Gíup mình với cảm ơn các bạn nhiều!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AEMF có
AE//MF
AF//ME
=>AEMF là hình bình hành
Để MA là phân giác của góc EMF thì AEMF là hình thoi
=>AM là phân giác của góc BAC
=>M là chân đường phân giác kẻ từ A xuống BC

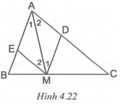
Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A
Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A


Đầu tiên, ta có EF//AB và EH//AC. Theo định lí Thales, khi có hai đường thẳng song song cắt qua các đường thẳng tạo ra các đoạn thẳng có tỉ số bằng nhau, ta có thể kết luận rằng các đoạn thẳng tạo ra bởi các đường thẳng song song đó cũng có tỉ số bằng nhau. Vì vậy, ta có:
EF/AB = EH/AC
Tiếp theo, ta sẽ sử dụng định lí Bồi thường. Theo định lí Bồi thường, khi có hai đường thẳng song song cắt qua một đường thẳng, các đoạn thẳng tạo ra bởi các đường thẳng song song đó và đường thẳng cắt qua có tỉ số bằng nhau, thì các đoạn thẳng tạo ra bởi các đường thẳng song song đó cũng có tỉ số bằng nhau. Vì vậy, ta có:
FH/BC = EH/AC
Vì EF//AB và FH/BC = EH/AC, ta có FH//BC.

a) Ta có: \(BC^2=13^2=169\)
\(AB^2+AC^2=5^2+12^2=169\)
Do đó: \(BC^2=AB^2+AC^2\)(=169)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Em nhập lại câu hỏi nha
em nhập lại rồi đó
anh f5 đi