Cho
d1 : y = x + 1
d2 : y = 5x - 3
d3 : y = mx + 4
Tìm m để 3 đoạn thẳng trên cùng đi qua 1 điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: (d2): y=3x-2y=1 => y: 3x-2y-1
Phương trình tung độ giao điểm của (d1) và (d2) là:
3x-2 = 3x-2y-1 => 3x-3x+2y=-1+2 => 2y=1 => y = 1/2
=> x = (1/2+2):3 = 5/6
Vậy (d1) và (d2) cùng đi qua điểm C(5/6; 1/2)
Thay x = 5/6 và y = 1/2 vào (d3) ta được: 1/2 = (m-2).5/6+2m-3
=> 1/2 = 5/6m - 5/3 + 2m - 3
=> 31/6 = 17/6 m
=> m = 31/17
Vậy m = 31/17 thì 3 đường thẳng (d1);(d2);(d3) cùng đi qua 1 điểm

b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2

Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x+3=x-4\\y=x-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=-4-3=-7\\y=x-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-7\\y=-7-4=-11\end{matrix}\right.\)
Thay x=-7 và y=-11 vào (d3), ta được:
-7m+m+1=-11
=>-6m=-11-1=-12
=>m=12/6=2

a: 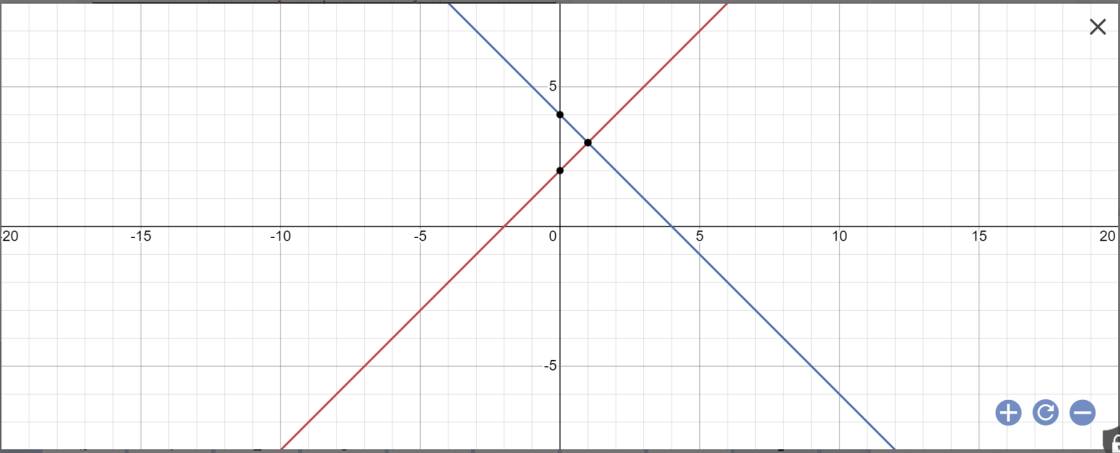
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Xét pthđ giao điểm của d1 và d2
x-4=2x+3
<=> x= -7
Thay x=-7 vào d1
y=-7-4=-11 => A(-7:-11) là giao điểm d1 và d2
Thay x=-7 vào d3 -> y=m(-7)+m+1=-6m+1=-11
- Để d1 d2 d3 đq -> A \(\in\)d3
-> -6m+1=-11
-6m=-12
m=2
Vậy m=2 thì 3 đường thẳng d1 , d2 , d3 đq
chúa bạn học tốt

a. PTTDGD của (d1) và (d2):
\(-2x=x-3\)
\(\Rightarrow x=1\)
Thay x = 1 vào (d1): \(y=-2\cdot1=-2\)
Vậy (d1) cắt (d2) tại điểm A(1;-2)
Lời giải:
a. PT hoành độ giao điểm: $-2x=x-3$
$\Leftrightarrow x=1$
$y=-2x=1(-2)=-2$
Vậy giao điểm của $(d_1), (d_2)$ là $(1,-2)$
b.
Để $(d_1), (d_2), (d_3)$ đồng quy thì $(d_3)$ cũng đi qua giao điểm của $(d_1), (d_2)$
Tức là $(1,-2)\in (d_3)$
$\Leftrightarrow -2=m.1+4\Leftrightarrow m=-6$
Giao của d1 và d2 có hoành độ thỏa mãn phương trình:
\(x\) + 1 = 5\(x\) - 3
5\(x\) - \(x\) = 1 + 3
4\(x\) = 4
\(x\) = 1
Thay \(x\) = 1 vào phương trình đường thẳng d1 ta có: y = 1 + 1 =2
Vậy d1 và d2 giao nhau tại A(1; 2)
Để d1; d2; d3 cùng đi qua 1 điểm thì:
Đường thẳng d3 phải đi qua A(1;2)
d3 đi qua A(1; 2) ⇔ tọa độ điểm A thỏa mãn phương trình đường thẳng d3
Thay tọa độ điểm A vào phương trình đường thẳng d3 ta có:
m.1 + 4 = 2
m = 2 - 4
m = -2
Kết luận: Với m = - 2 thì đường thẳng d3 có dạng y = -2\(x\) + 4 và cắt hai đường thẳng d1; d2 tại 1 điểm A(1; 2)
Pt hoành độ giao điểm của d1 và d2 là \(x+1=5x-3\Leftrightarrow4x=4\Leftrightarrow x=1\) \(\Rightarrow y=x+1=1+1=2\). Vậy d1 cắt d2 tại điểm \(A\left(1;2\right)\). Để 3 đường thẳng trên cùng đi qua 1 điểm thì d3 phải đi qua A. Điều này tương đương với \(2=m+4\Leftrightarrow m=-2\)