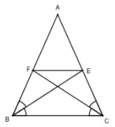
Cho tam giác ABC cân tại A,các đường phân giác BE,CF
a,cmBFEC là hình thang cân
b,cmBF=FE=EC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác AFC và tam giác AEB có :
góc A chung
AB = AC (gt)
góc B1 = góc C1 (gt)
=>tam giác AFC = tam giác AEC (g.c.g)
=>FC = EB (đcpcm)
b)Vì tam giác AFC = tam giác AEC (cmt)
=>AF=AE (hai cạnh tương ứng )
=>tam giác AFE cân tại A
=>góc AFE=180 độ - góc A : 2
mặt khác ta có : tam giác ABC cân tại A
=>góc B =180 độ - góc A : 2
=>góc B = góc AFE
góc B và góc AFE ở vị trí đồng vị
=>EF song song BC
=>FBCE là hình thang
=>FB = EC
mà góc B =góc C (gt)
=>FBCE là hình thang cân
Ta có :FE song song BC
=>góc EBC = góc FEB (SLT)
mà góc FBE = góc EBC (gt)
=>góc FBE = góc FEB
=>tam giác BFE cân tại F
=>EF=FB (hai cạnh tương ứng ) (đcpcm)
ta lại có :
FB=FC(cmt)
=>EC=FE (đcpcm)
Bn nhớ k cho mình nha!!!!!!!!

Tớ nói với cậu chỗ tin nhắn rồi .... nếu không hiểu thì báo tớ,,,,, tớ ns tiếp cho

+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
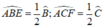
Mà tam giác ABC cân tại A nên ∠ B = ∠ C
Suy ra: ∠ ABE = ∠ ACF
Xét hai tam giác AEB và AFC
Có AB = AC ( ∆ ABC cân tại A)
∠ ABE = ∠ ACF (chứng minh trên)
∠ A là góc chung
⇒ ∆ AEB = ∆ AFC (g.c.g) ⇒ AE = AF ⇒ ∆ AEF cân tại A
⇒ ∠ AFE = ( 180 0 − ∠ A) / 2 và trong tam giác ∆ ABC: ∠ B = ( 180 0 − ∠A) / 2
⇒ ∠ AFE = ∠ B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: ∠ FEB = ∠ EBC (so le trong)
Lại có: ∠ FBE = ∠ EBC ( vì BE là tia phân giác của góc B)
⇒ ∠ FBE = ∠ FEB
⇒ ∆ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)

Góc BEC=góc BFC=90 độ
=>BCEF LÀ TỨ GIÁC NỘI TIẾP
=>Góc AFE=gócC (1)
Tam giác BNC đồng dạng với tam giác BMC(g.c.g)
=>Góc BNC=góc BMC
=>BCMN là tứ giác nội tiếp
=>Góc ANM=góc AMN=góc C (2)
Từ 1 và 2
Có EF song song với MN và góc ANM=góc AMN
=>EMNF là hình thang cân
a)Ta có: BE, CF là pgiac(gt)
=> ∠CBE=∠FEB\(=\dfrac{1}{2}\widehat{ABC}\)
\(\widehat{BCF}=\widehat{ECF}=\dfrac{1}{2}\widehat{ABC}\)
Mà ∠ABC=∠ACB(tam giác ABC cân tại A); ∠BCF=∠CBE(cmt)
Ta có: xét tam giác BFC và tam giác CEB có:
+∠FBC=∠ECB (tam cân)
+BC chung
+∠BCF=∠CBE(cmt)
=> tam giác BFC=tam giác CEB (g.c.g)
=>BF=CE(2 cạnh tương ứng)
Mà AB=AC(gt)
=>AB-BC=AC-CE
=>AF=AE
=>tam giác AFE cân tại A
=> \(\widehat{AFE}=\dfrac{1}{2}\left(180^o-\widehat{A}\right)\)
Mà ∠ABC=1/2(180-A)
=>∠AFE=∠ABC
Mà 2 góc ở vị trí đồng vị
=>EF//BC
=>BFEC là hình thang
Mà ∠CBF=BCE(tam giác cân)
=>BFEC là hình thang cân)
b) Do BFEC là hình thang cân
=>FE//BC; BF=CE(1)
=>góc FEB= góc EBC
Mà BE là pgiac góc B
=>góc FBE=FEB
=> tam giác FBE cân
=>BF=FE (2)
Từ(1);(2)=>BF=FE=EC