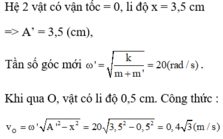Hệ dao động quả cầu lò xo k = 100 N/m và quả cầu khối lượng m = 1 kg. Tại vị trí cân bằng người ta kéo quả để lò xo dãn một đoạn 10 cm thả nhẹ. Viết phương trình li độ của quả cầu chọn chiều dương cùng với chiều kéo vật góc tọa độ tại vị trí cân bằng góc thời gian khi thả vật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AM
Ami Mizuno
26 tháng 7 2023
Đúng(2)
Những câu hỏi liên quan
VT
25 tháng 3 2017
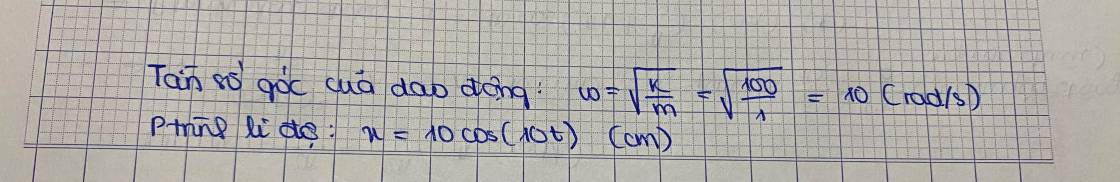
Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Cách giải:
Tần số góc: ω = k m = 20 r a d / s
Kéo quả cầu xuống dưới vị trí cân bằng một đoạn 2cm rồi buông nhẹ cho dao động điều hoà => Biên độ dao động A = 2cm.
Chọn trục toạ độ Ox có gốc O là vị trí cân bằng, chiều dương hướng lên trên, gốc thời gian lúc buông vật
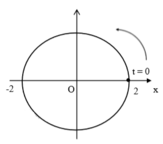
=> Pha ban đầu : φ = 0
Vậy PT dao động x = 2cos(20t)cm
VT
21 tháng 4 2018
Đáp án A
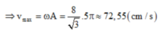
∆ l 01 = m g k = 2 c m
ω = k m = 10 5 rad/s
∆ l 02 = m ' g k = 2 , 5 c m
Tại VTCB sau đó , lò xo giản 2,5 cm , tại thời điểm quả cầu tới biên dưới O lò xo giản 6 cm
=> A' = (6-2,5) = 3,5 cm; ω 2 = k m ' = 20
Vị trí O ban đầu cách VTCB lúc sau 0,5 cm
15 tháng 7 2016
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)
HT
20 tháng 3 2021
a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)
