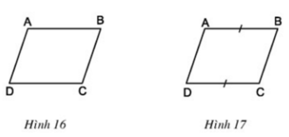
chi hình thang ABCD có AB//CD, AD=BC Chững minh AB=CD, AD//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 11 2017
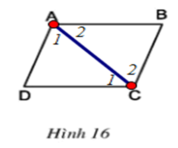
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
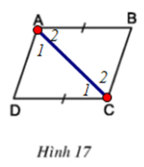
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
KT
3 tháng 8 2018
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC
21 tháng 6 2023
Qua P kẻ đường thẳng song song với AD cắt CD tại P. Khi đó dễ thấy \(AB=DP\). Từ đó \(DC-AB=DC-DM=CM\)
Mặt khác, \(AD=BM\) nên \(AD+BC=BM+BC\).
Hiển nhiên \(CM< BM+BC\). Điều này dẫn đến \(DC-AB< AD+BC\) (đpcm)
29 tháng 5 2016
a) Ta có : AB // CD ( do ABCD là hình thang )
AD // BC ( gt )
=> ABCD là hình bình hành
=> AD = BC ; AB = CD
b) Ta có : AB = CD ( gt )
AB // CD ( gt )
=> ABCD là hình bình hành
=> AD // BC ; AD = BC
21 tháng 9 2021
Kẻ BM//AD( \(M\in AD\))
Xét tứ giác ABMD có:
BM//AD(cách vẽ)
AB//DM( do AB//CD, \(M\in DC\))
=> Tứ giác ABMD là hình bình hành
=> AD=BM và AB=DM
Ta có: DM+MC=DC
=> AB+MC=DC
=> MC=DC-AB = 7-4=3cm
Xét tam giác BMC có:
BM + BC > MC( bất đẳng thức trong tam giác)
Mà BM=AD, MC= 4cm
=> AD+BC >4cm
PS
0
PN
0