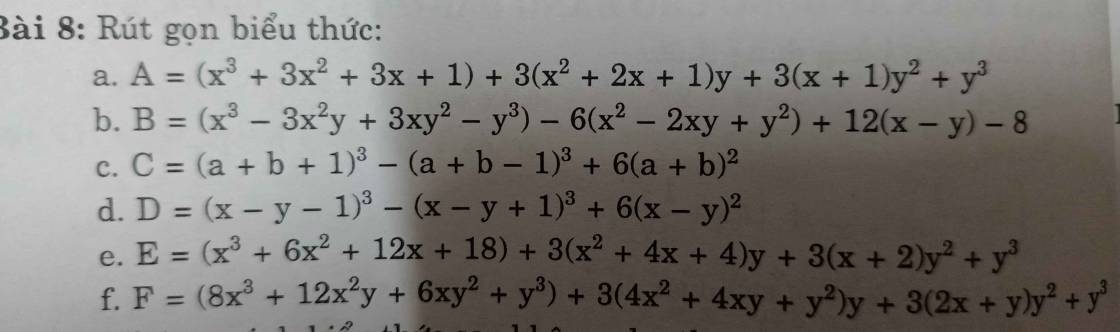giúp e câu b,f với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
5
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
HK
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
2
5 tháng 2 2022
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
21 tháng 10 2021
e) \(sin^22x-6sin2x+5=0\Rightarrow\) \(\left[{}\begin{matrix}sin2x=5\left(loại\right)\\sin2x=1\end{matrix}\right.\)
\(\Rightarrow sin2x=sin\left(\dfrac{\pi}{2}\right)\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
f.
\(4cos^23x-2\left(\sqrt{3}+1\right)cos3x+\sqrt{3}=0\)
\(\Leftrightarrow4cos^23x-2cos3x-2\sqrt{3}cos3x+\sqrt{3}=0\)
\(\Leftrightarrow2cos3x\left(2cos3x-1\right)-\sqrt{3}\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left(2cos3x-\sqrt{3}\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\\cos3x=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
TT
23 tháng 4 2021
d) \(\dfrac{5x+2}{6}\) +\(\dfrac{3-4x}{2}\) = 2-\(\dfrac{x+7}{3}\)
=>5x+2+3(3-4x)=12-2(x+7)
5x+2+9-12x=12-2x-14
-5x=-13
x=\(\dfrac{13}{5}\)
e) \(\dfrac{-20}{9}x +4=\dfrac{8}{3}x-40\)
=>-20x+36=24x-360
-44x=-396
x=9
f) 3x(2x-5)-4X+10=0
6X2 -15X-4X+10=0
2x(3x-2)-5(3x-2)=0
(3x-2)(2x-5)=0
\(\left[\begin{array}{} Biểu thức (3x-2=0)\\ Biểu thức (2x-5=0) \end{array} \right.\)\(\left[\begin{array}{} (x=\dfrac{2}{3})\\ (x=\dfrac{5}{2}) \end{array} \right.\)
j) \(\dfrac{x-45}{55}+\dfrac{x-47}{53}=\dfrac{x-55}{45}+\dfrac{x-53}{47}\)
\(\dfrac{x-45}{55}-1+\dfrac{x-47}{53}-1=\dfrac{x-55}{45}-1+\dfrac{x-53}{47}-1\)
\(\dfrac{x-100}{55}+\dfrac{x-100}{53}=\dfrac{x-100}{45}+\dfrac{x-100}{47}\)
\(\dfrac{x-100}{55}+\dfrac{x-100}{53}-\dfrac{x-100}{45}-\dfrac{x-100}{47}=0\)
(x-100)(\(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\))=0
=> x-100=0(\(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\) >0)
=> x= 100
4 tháng 9 2023
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
18 tháng 1 2023
b: =>(x+1)(x-1)-(x+3)(x-3)=2x^2+6x
=>2x^2+6x=x^2-1-x^2+9=8
=>2x^2+6x-8=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1(loại)
a: =>x^3+2x-2x(x^2+1)=0
=>x^3+2x-2x^3-2x=0
=>-x^3=0
=>x=0(nhận)
c: =>(x-2)(x+2)-(x+5)^2=x^2-8
=>x^2-4-x^2-10x-25=x^2-8
=>x^2-8=-10x-29
=>x^2+10x+21=0
=>(x+3)(x+7)=0
=>x=-3 hoặc x=-7
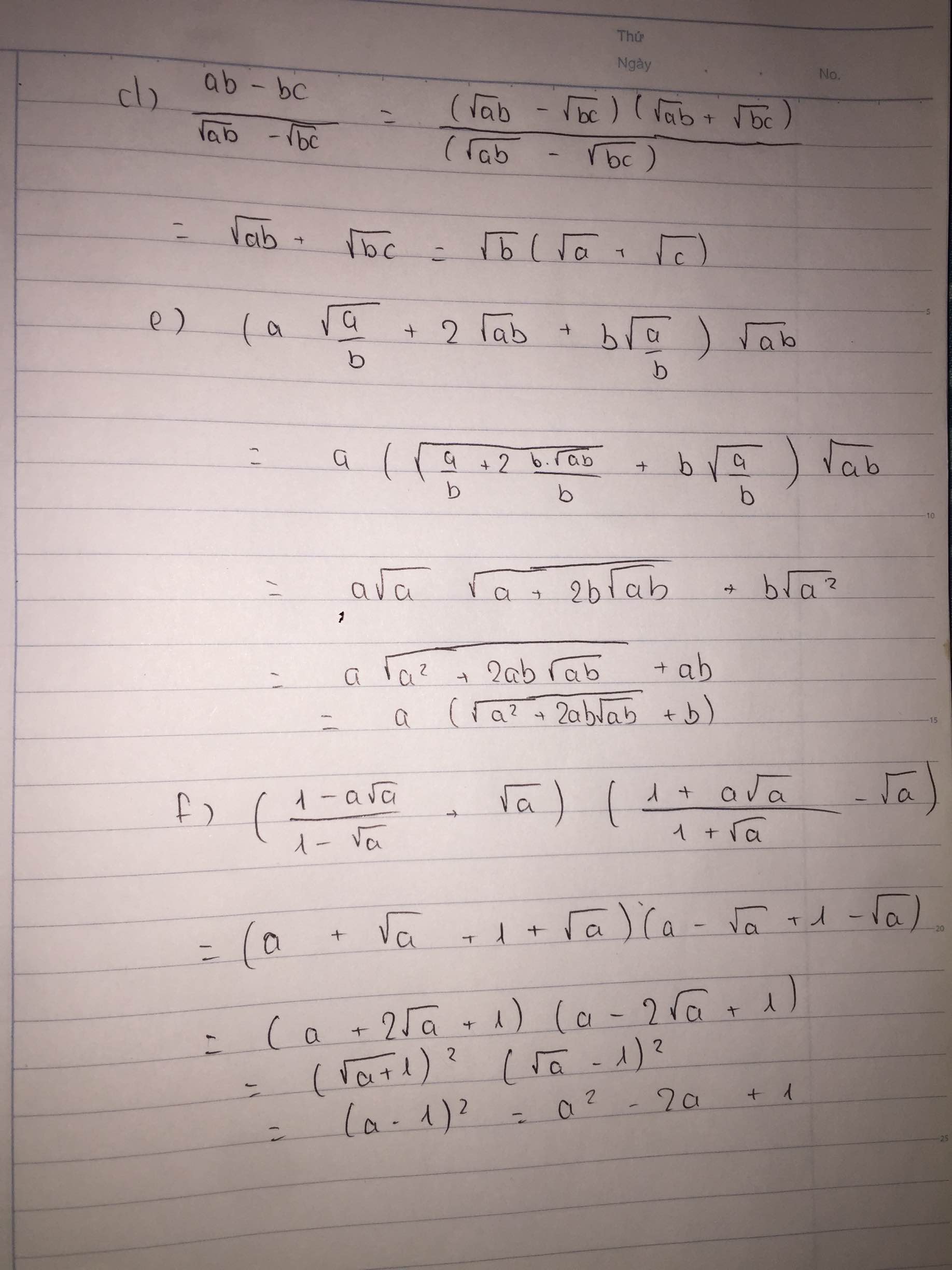
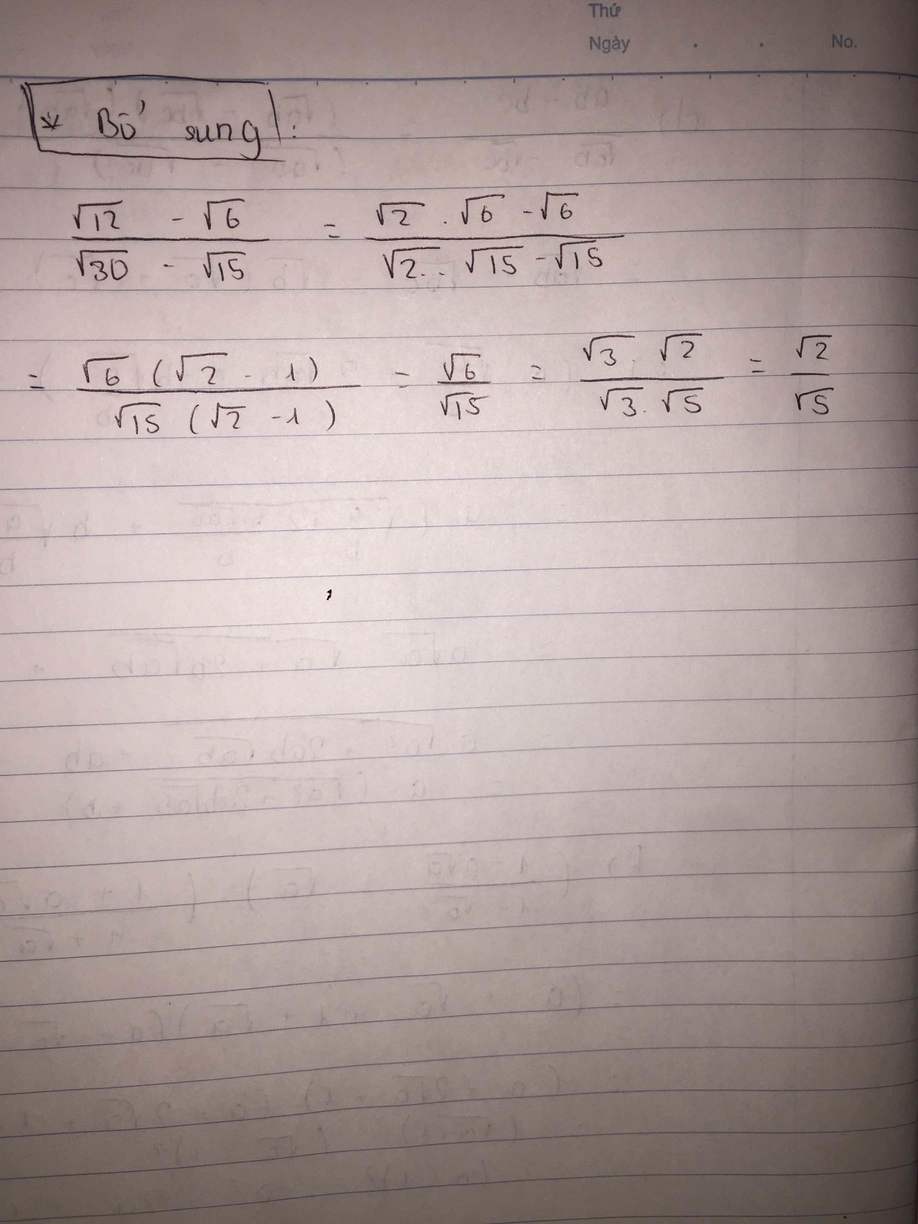
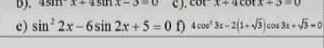
b) \(B=\left(x^3-3x^2y+3xy^2-y^3\right)-6\left(x^2-2xy+y^2\right)+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-6\left(x-y\right)^2+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-3\cdot2\cdot\left(x-y\right)^2+3\cdot2^2\cdot\left(x-y\right)-2^3\)
\(B=\left[\left(x-y\right)-2\right]^3\)
\(B=\left(x-y-2\right)^3\)
f) \(F=\left(8x^3+12x^2y+6xy^2+y^3\right)+3\left(4x^2+4xy+y^2\right)y+3\left(2x+y\right)y^2+y^3\)
\(F=\left(2x+y\right)^3+3\left(2x+y\right)^2y+3\left(2x+y\right)y^2+y^3\)
\(F=\left[\left(2x+y\right)+y\right]^3\)
\(F=\left(2x+y+y\right)^3\)
\(F=\left(2x+2y\right)^3\)
b: =(x-y)^3-6(x-y)^2+12(x-y)-2^3
=(x-y-2)^3
f: =(2x+y)^3+3(2x+y)^2*y+3*(2x+y)*y^2+y^3
=(2x+y+y)^3
=(2x+2y)^3