tính những hằng đẳng thức
x4+y8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
3
A
1
16 tháng 6 2017
\(\frac{1}{27}-64t^3=\left(\frac{1}{3}\right)^3-\left(4t\right)^3=\left(\frac{1}{3}-4t\right)\left(\frac{1}{9}+\frac{4}{3}t+16t^2\right)\)
H9
HT.Phong (9A5)
CTVHS
21 tháng 8 2023
a. \(x^2-10x+25=\left(x-5\right)^2\)
b.\(4-4x^2+x^4=\left(2-x^2\right)^2\)
c. \(x^2-6y+9y^2=\left(x-3y\right)^2\)
d. \(\left(2x+y^2\right)\left(2x-y^2\right)=4x^2-y^4\)
CM
20 tháng 8 2019
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm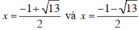 
Ta có bảng xét dấu sau:
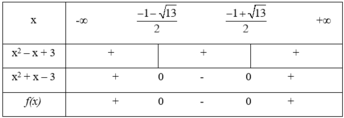
Kết luận:
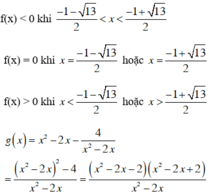
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
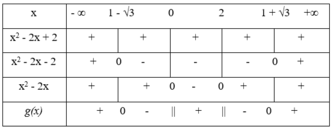
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
19 tháng 7 2019
Trả lời
2002 x 1006
= ( 1504 + 498 ) x ( 1504 - 498 )
= 15042 - 4982
= 2014012
198 x 202
= ( 200 - 2 ) x ( 200 + 2 )
= 2022 - 22
= 40800
CM
29 tháng 6 2019
a) Kết quả - x 2 + 2. b) Kết quả − 1 2 ( 4 x 2 + 10 x + 25 ) .
c) Kết quả - ( x 3 + 1 ) 2 .
MN
2
26 tháng 9 2018
Ta có:
\(101^{^{ }3}\) = \(\text{(100+1)^3}\) : \(99^3\)= \(\text{(100-1)^3}\)
26 tháng 9 2018
\(101^3-99^3+1\)
\(=\left(101-99\right)\left(101^2+101.99+99^2\right)+1\)
\(=2.\left[\left(101+99\right)^2-101.99\right]+1\)
\(=2.\left[40000-9999\right]+1\)
\(=2.30001+1=60003\)
Mình nghĩ cách này là thuận tiện nhất rồi. Chúc bạn học tốt.