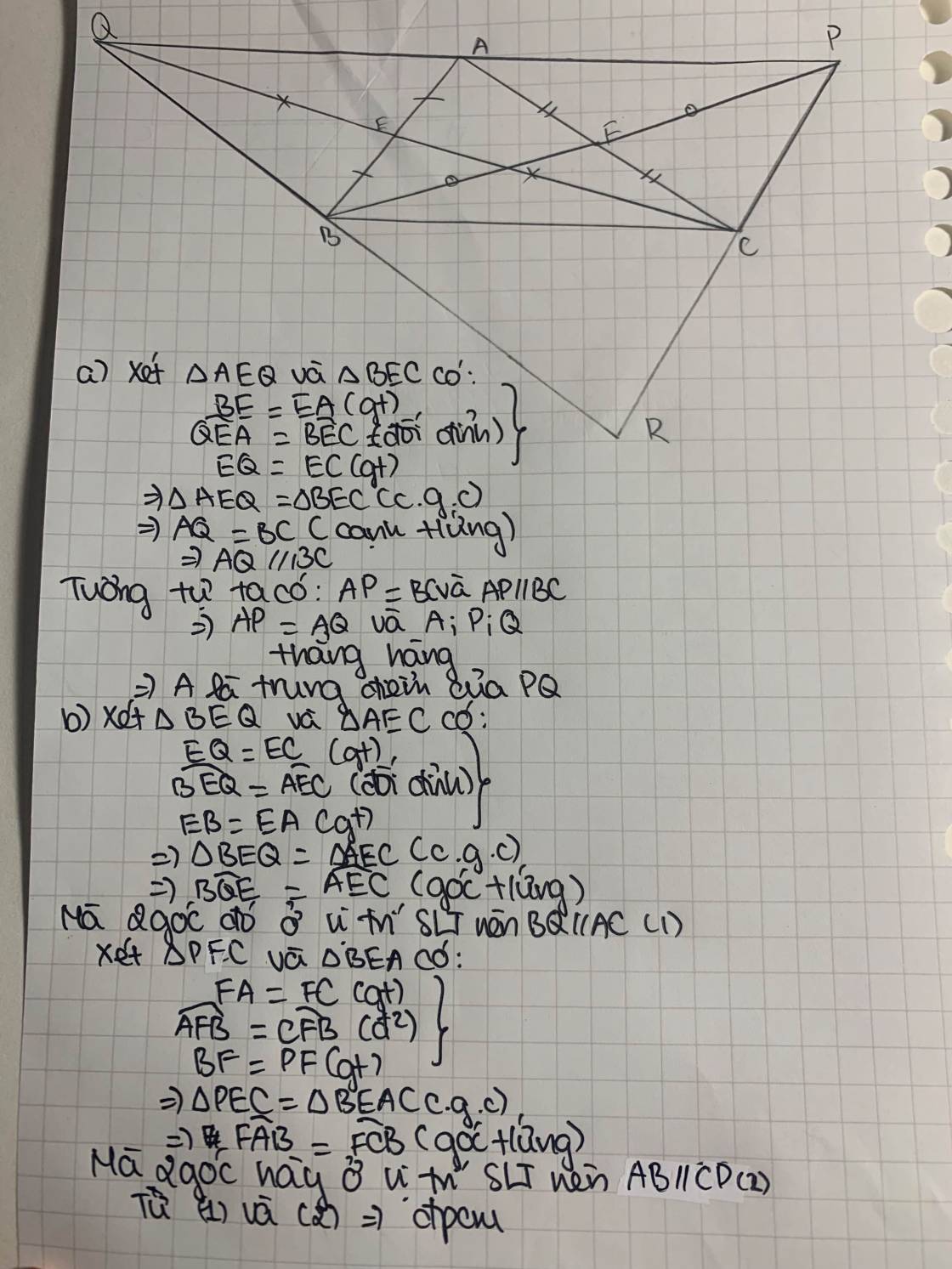
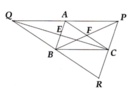
Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của AB, AC. Trên tia đối của tia FB lấy P sao cho PF = BF. Trên tia đối của tia EC lấy điểm Q sao cho QE = CE.
a) Chứng minh A là trung điểm của PQ.
b) Chứng minh BQ // AC và CP // AB.
c) Gọi R là giao điểm của hai đường thẳng PC và QB. Chứng minh chu vi tam giác PQR bằng hai lần chu vi tam giác ABC.
d) Chứng minh AR, BP,CQ đồng quy tại một điểm.