Cho tam giác ABC vuông tại A.Trên cạnh BC lấy điểm sao cho BD=BA.Tia phân giác của góc ABC cắt cạnh AC tại ECho tam giác ABC vuông tại A.Trên cạnh BC lấy điểm sao cho BD=BA.Tia phân giác của góc ABC cắt cạnh AC tại E
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 1 2021
Xét ΔDBE và ΔABE có
BA=BD(gt)
\(\widehat{ABE}=\widehat{DBE}\)(BE là tia phân giác của \(\widehat{ABD}\))
BE chung
Do đó: ΔDBE=ΔABE(c-g-c)
⇒\(\widehat{BDE}=\widehat{BAE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BDE}=90^0\)
hay ED⊥BC tại D
Xét ΔCFB có
BH là đường cao ứng với cạnh CF(CH⊥BE, F∈CH, H∈BE)
CA là đường cao ứng với cạnh FB(CA⊥AB, F∈AB)
BH cắt CA tại E
Do đó: E là trực tâm của ΔCFB(Tính chất ba đường cao của tam giác)
⇒FE⊥BC
mà ED⊥BC
và FE,ED có điểm chung là E
nên D,E,F thẳng hàng(đpcm)
KV
8 tháng 3 2023
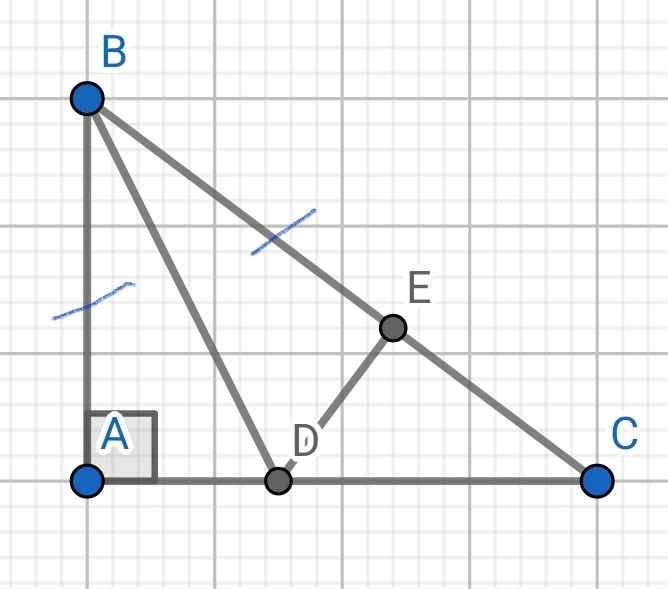
a) Xét ∆BAD và ∆BED có:
AB = BE (gt)
BD là cạnh chung
∠ABD = ∠EBD (do BD là phân giác của ABC)
⇒ ∆BAD = ∆BED (c-g-c)
b) Do ∆BAD = ∆BED (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BC
c) Do DE ⊥ BC (cmt)
⇒ ∠DEC = 90⁰
⇒ ∆DEC vuông tại E
⇒ DC là cạnh huyền
⇒DE < DC (1)
Do ∆BAD = ∆BED (cmt)
⇒ AD = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒AD < DC
11 tháng 12 2021
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
11 tháng 12 2021
\(d,\) Gọi \(AE\cap BD=\left\{H\right\}\)
\(\left\{{}\begin{matrix}\widehat{ABH}=\widehat{EBH}\\AB=AE\\BH\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABH=\Delta EBH\left(c.g.c\right)\\ \Rightarrow\widehat{BHA}=\widehat{BHE}\\ \text{Mà }\widehat{BHE}+\widehat{BHA}=180^0\left(\text{kề bù}\right)\\ \Rightarrow\widehat{BHE}=\widehat{BHA}=90^0\\ \Rightarrow BH\bot AE\\ \Rightarrow BD\bot AE\)
23 tháng 12 2023
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
c: Xét ΔDAM vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAM=ΔDEC
=>DM=DC
TM
24 tháng 2 2021
hình tự vẽ, c,d tự làm tiếp, bài này đơn giản nha.
a/ Xét ΔABD và ΔEBD vuông tại A và E có:
BD chung; AB = EB; góc A=E=90o
=> ΔABD = ΔEBD (...)
=> góc ABD = góc EBD
=> BD là phân giác của góc ABC
b,xét tam giác BEK vuông tại Evà tam giác BACvuông tại E , có BE=BA, góc KBC chung
=>tam giac BEK= tam giac BAC (ch-gn)
24 tháng 2 2021
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
BA=BE(gt)
Do đó: ΔABD=ΔEBD(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABD}=\widehat{EBD}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{ABD}=\widehat{CBD}\)
mà tia BD nằm giữa hai tia BA,BC
nên BD là tia phân giác của \(\widehat{ABC}\)(đpcm)
4 tháng 7 2023
1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC