Cho tam giác ABC cân tại A .Kẻ AD vuông góc với BC ,trên cạnh AD lấy điểm E là trung điểm của AD .Kẻ DK vuông góc với BE .Cm: góc AKC vuông góc tại K
Giúp tớ nha !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔADB=ΔAEC
=>AD=AE
=>ΔADE cân tại A
b,c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc MAB=góc NAC(góc MAB=góc MAC+góc BAC;góc NAC=góc NAB+góc BAC;gócMAC=góc NAB)
=>ΔAMB=ΔANC
=>BM=CN
d: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
=>HK//BC
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
Câu hỏi của Bảo Châu Trần - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại đây nhé.
25 tháng 12 2021
Đáp án:
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC
cho xin tích ạ
27 tháng 1 2022
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC
25 tháng 12 2021
Đáp án:
Giải thích các bước giải:
a) tam giác ADC và tam giác ECD
AD=FC
chung cạnh CD
Góc D=góc C= 90 độ
suy ra tam giác ADC=tam giác ECD(c.g.c)
b) Ta có AD=CE
AD // CF ( cùng vuông góc BC)
suy ra ADEC là hình bình hành
suy ra DE // AC
mà AB vuông góc AC => DE vuông góc AB
c) Ta có ADEC là hình bình hành => góc DEC=góc DAC (1)
Ta có góc DAC+góc BAD= 90 độ
mà góc ABC+ góc BAD= 90 độ
=> góc DAC=ABC (2)
Từ (1) và (2) suy ra góc CED=góc ABC
cho xin tích ạ
KV
10 tháng 1
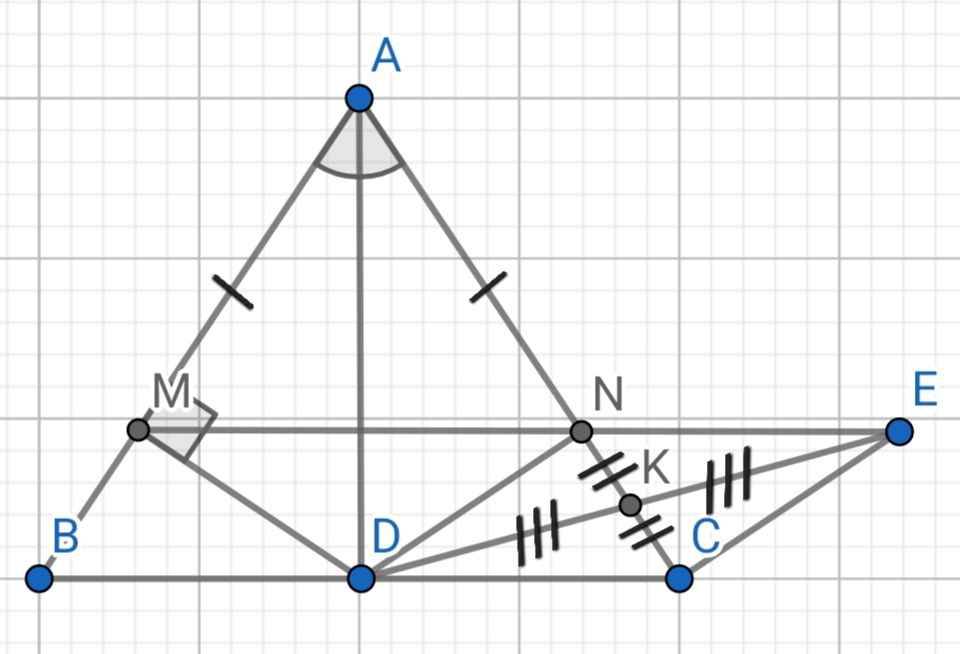a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng
6 tháng 1 2022
a: Xét ΔABD và ΔACE có
AB=AC
ˆABD=ACE^
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và ˆD=ˆED^=E^
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
ˆD=E^
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
ˆHAB=KAC^
Do dó: ΔABH=ΔACK
LD
4 tháng 12 2017
Gọi N, H lần lượt là trung điểm của BM và DM.
Xét tam giác ABC cân tại A ta có:
AD là đường cao (gt)
=> AD là đường trung tuyến của tam giác ABC
=> D trung điểm BC
Xét tam giác BMC ta có:
N trung điểm BM (cách vẽ)
D trung điểm BC (cmt)
=> ND là đường trung bình của tam giác BMC
=> ND // MC
Xét tam giác AMD ta có:
H trung điểm MD (cách vẽ)
E trung điểm AD (gt)
=> HE là đường trung bình của tam giác AMD
=> HE // AM
Xét tam giác BMD ta có:
N trung điểm MB (cách vẽ)
H trung điểm MD (cách vẽ)
=> NH là đường trung bình của tam giác BMD
=> NH // BD
Mà BD _|_ AD tại D (AD là đường cao của tam giác ABC)
Nên NH _|_ ED (E thuộc AD)
Xét tam giác BDE ta có:
DM là đường cao (DM _|_ BE tại M)
NH là đường cao (NH _|_ ED)
DM cắt NH tại H (gt)
=> H là trực tâm của tam giác BED
=> EH là đường cao thứ 3 của tam giác BED
=> EH _|_ ND
Mà ND // MC (cmt)
Nên EH _|_ MC
Mặt khác EH // AM (cmt)
=> AM _|_ MC tại M (đpcm)