Tìm x
x5(3x-1)m+3 : x5(3x-1)m-1 - 56 : 52=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 8 2017
Ta có
P ( x ) = 2 x 3 − 3 x + x 5 − 4 x 3 + 4 x − x 5 + x 2 − 2 = x 5 − x 5 + 2 x 3 − 4 x 3 + x 2 + ( 4 x − 3 x ) − 2 = − 2 x 3 + x 2 + x − 2 Và Q ( x ) = x 3 − 2 x 2 + 3 x + 1 + 2 x 2 = x 3 + − 2 x 2 + 2 x 2 + 3 x + 1 = x 3 + 3 x + 1
Khi đó
M ( x ) = P ( x ) + Q ( x ) = − 2 x 3 + x 2 + x − 2 + x 3 + 3 x + 1 = − 2 x 3 + x 2 + x − 2 + x 3 + 3 x + 1 = − 2 x 3 + x 3 + x 2 + ( x + 3 x ) − 2 + 1 = − x 3 + x 2 + 4 x − 1
Bậc của M ( x ) = - x 3 + x 2 + 4 x - 1 l à 3
Chọn đáp án C
10 tháng 12 2023
a: \(575-\left(2x+70\right)=445\)
=>\(2x+70=575-445=130\)
=>\(2x=130-70=60\)
=>x=60/2=30
b: \(575-2\left(x+70\right)=445\)
=>\(2\left(x+70\right)=575-445=130\)
=>x+70=130/2=65
=>x=65-70=-5
c: \(x^5=32\)
=>\(x^5=2^5\)
=>x=2
d: \(\left(3x-1\right)^3=8\)
=>\(\left(3x-1\right)^3=2^3\)
=>3x-1=2
=>3x=3
=>\(x=\dfrac{3}{3}=1\)
e: \(\left(x-2\right)^3=27\)
=>\(\left(x-2\right)^3=3^3\)
=>x-2=3
=>x=5
f: \(\left(2x-3\right)^2=9\)
=>\(\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
g: \(2x+5=3^4:3^2\)
=>\(2x+5=3^2\)
=>2x+5=9
=>2x=9-5=4
=>x=4/2=2
h: \(\left(4x-5^2\right)\cdot7^3=7^4\)
=>\(4x-25=\dfrac{7^4}{7^3}=7\)
=>4x=25+7=32
=>\(x=\dfrac{32}{4}=8\)
CM
1 tháng 9 2018
c. Thay x = -1 vào A(x) và B(x) ta có:
A(-1) = 0, B(-1) = 2
Vậy x = -1 là nghiệm của A(x) nhưng không là nghiệm của B(x) (1 điểm)
26 tháng 1 2021
a, làm tương tự với phần b bài nãy bạn đăng
b, \(\left(x+1\right)^2-5=x^2+11\)
\(\Leftrightarrow x^2+2x+1-5=x^2+11\)
\(\Leftrightarrow2x-10=0\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là S = { 5 } ( kết luận như thế với các phần sau nhé ! )
c, \(3\left(3x-1\right)=3x+5\Leftrightarrow9x-3-3x-5=0\)
\(\Leftrightarrow6x-8=0\Leftrightarrow x=\frac{4}{3}\)
d, \(3x\left(2x-3\right)-3\left(3+2x^2\right)=0\)
\(\Leftrightarrow6x^2-9x-9-6x^2=0\Leftrightarrow-9x=9\Leftrightarrow x=-1\)
e, khai triển nó ra rút gọn rồi giải thôi nhé! ( tự làm )
f, \(\left(x-1\right)^2-x\left(x+1\right)+3\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-2x+1-x^2+x+3x-6+5=0\)
\(\Leftrightarrow2x=0\Leftrightarrow x=\frac{0}{2}\)vô lí
Vậy phương trình vô nghiệm
CM
5 tháng 12 2017
Ta có
P ( x ) = 2 x 3 − 3 x + x 5 − 4 x 3 + 4 x − x 5 + x 2 − 2 = x 5 − x 5 + 2 x 3 − 4 x 3 + x 2 + ( 4 x − 3 x ) − 2 = − 2 x 3 + x 2 + x − 2 Và Q ( x ) = x 3 − 2 x 2 + 3 x + 1 + 2 x 2
= x 3 + - 2 x 2 + 2 x 2 + 3 x + 1 = x 3 + 3 x + 1
Khi đó
P ( x ) − Q ( x ) = − 2 x 3 + x 2 + x − 2 − x 3 + 3 x + 1 = − 2 x 3 + x 2 + x − 2 − x 3 − 3 x − 1 = − 2 x 3 − x 3 + x 2 + ( x − 3 x ) − 2 − 1 = − 3 x 3 + x 2 − 2 x − 3
Chọn đáp án B
KT
1
DG
2
B
3 tháng 9 2021
Đặt A=(2+x)5(3x-1)7
khai triển ta có:A=(\(_{k=0}^5\Sigma C_5^k2^{5-k}x^k\)).(\(^7_{i=0}\Sigma C_7^i\left(3x\right)^i\))
=\(\left(_{k=0}^5\Sigma\right)\left(_{i=0}^7\Sigma\right)\left(C_5^kC^i_7\right)\left(x^k.\left(3x\right)^i\right)\)
=số hạng\(\left(C_5^kC^i_7\right)\left(x^k.\left(3x\right)^i\right)\)chứa x5 tại k+i=5
có k\(\in\){0,1,2,...5},i\(\in\){0,1,2,...7}
=>(k,i)={(0,5);(1,4);(2,3);(3,2);(4,1);(5,0)}
=>Hệ số của x5 là:\(\left(C_5^0C^5_7\right)3^5\)+\(\left(C_5^1C^4_7\right)\left(3^4\right)\)+\(\left(C_5^2C^3_7\right)\left(3^3\right)\)+\(\left(C_5^3C^2_7\right)\left(3^2\right)\)+
\(\left(C_5^4C^1_7\right)\left(3^1\right)\)+\(\left(C_5^5C^0_7\right)3^0\)=30724
Hok tốt!!!
CM
24 tháng 8 2017
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
CM
27 tháng 8 2017
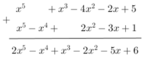
Hệ số của x5 trong khai triển x(1-2x)5 là (-2)4.C54
Hệ số của x5 trong khai triển x2(1+3x)10 là 33.C103
Do đó hệ số của x5 trong khai triển x(1-2x)5+ x2(1+3x)10 là
(-2)4.C54 + 33.C103= 3320
Chọn C
HA
1
3 tháng 5 2022
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)