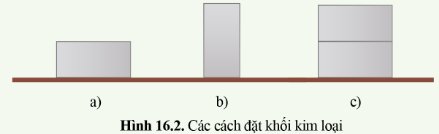
So sánh áp suất do khối kim loại tác dụng lên cát trong trường hợp ở hình 16.2a với 16.2b và 16.2c.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
- Với cùng một áp lực (hình 16.2a, b), diện tích bị ép giảm: độ lún trong hình 16.2b lớn hơn, vậy với cùng một áp lực, khi giảm diện tích bị ép sẽ làm tăng áp suất lên.
- Trên một diện tích bị ép không đổi (hình 16. a, c), tăng áp lực: độ lún trong hình 16.2c lớn hơn, vậy với cùng một diện tích bị ép, khi tăng áp lực sẽ làm tăng áp suất lên.
VT
8 tháng 11 2019
Ta có:
- Cùng diện tích bị ép như nhau, nếu độ lớn của áp lực càng lớn thì tác dụng nó cũng càng lớn.
- Cùng độ lớn của áp lực như nhau, nếu diện tích bị ép càng nhỏ thì tác dụng của áp lực càng lớn.
Như vậy, tác dụng của áp lực phụ thuộc vào diện tích bị ép và độ lớn của áp lực.
Điền dấu:
| Áp lực (F) | Diện tích bị ép (S) | Độ lún (h) |
| F2 > F1 | S2 = S1 | h2 > h1 |
| F3 = F1 | S3 < S1 | h3 > h1 |
ND
Nguyễn Đức Trí
VIP
9 tháng 9 2023
a) Áp lực :
\(\dfrac{200}{1.1}=200\left(N/m^2\right)\)
b) Áp lực :
\(\dfrac{200}{2.1}=100\left(N/m^2\right)\)
18 tháng 1 2022
Áp lực cả 3 trường hợp đều như nhau nên:
\(F_1=F_2=F_3=P=10m=10.0,84=8,4\left(N\right)\)
TH1: Mặt tiếp xúc là \(5cm\times6cm\)
\(p_1=\dfrac{F}{S}=\dfrac{8,4}{0,05\left(m\right)\times0,06}=2800\left(\dfrac{N}{m^2}\right)\)
TH2: Mặp tiếp xúc là \(6cm\times7cm\)
\(p_2=\dfrac{F}{S}=\dfrac{8,4}{0,06\times0,07}=2000\left(\dfrac{N}{m^2}\right)\)
TH3: Mặt tiếp xúc là \(5cm\times7cm\)
\(p_3=\dfrac{F}{S}=\dfrac{8,4}{0,05\times0,07}=2400\left(\dfrac{N}{m^2}\right)\)
-->Áp lực do vật tác dụng lên mặt sàn đều như nhau nhưng áp suất trong cả 3 trường hợp đều khác nhau
\(p_A=\dfrac{F}{s_A};p_B=\dfrac{F}{s_B};p_C=\dfrac{2F}{s_C}\\ Mà:s_A>s_B;s_A=s_C\\ Vậy:\dfrac{F}{s_A}< \dfrac{F}{s_B}\Leftrightarrow p_A< p_B\\ 2.\dfrac{F}{s_A}=\dfrac{2F}{s_C}\Leftrightarrow p_A=\dfrac{1}{2}p_C\)