Cho nửa dg tròn tâm O dg kính MN TT MX Ny gọi A thuộc nửa dg tròn tâm O qua A vẽ tt dg tròn cắt Mx Ny tại E,F a CM tam giác EOF vuông b EF=ME+NF C OEF= 60 độ tính EFO Giúp mình v cần gấp chiều nay hc r
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,
1 Ta có ÐCAB = 900 ( vì tam giác ABC vuông tại A); ÐMDC = 900 ( góc nội tiếp chắn nửa đường tròn ) =>ÐCDB = 900 như vậy D và A cùng nhìn BC dưới một góc bằng 900 nên A và D cùng nằm trên đường tròn đường kính BC => ABCD là tứ giác nội tiếp.
ABCD là tứ giác nội tiếp => ÐD1= ÐC3( nội tiếp cùng chắn cung AB).
ÐD1= ÐC3 =>  => ÐC2 = ÐC3 (hai góc nội tiếp đường tròn (O) chắn hai cung bằng nhau)
=> ÐC2 = ÐC3 (hai góc nội tiếp đường tròn (O) chắn hai cung bằng nhau)
=> CA là tia phân giác của góc SCB.
2, Xét DCMB Ta có BA^CM; CD ^ BM; ME ^ BC như vậy BA, EM, CD là ba đường cao của tam giác CMB nên BA, EM, CD đồng quy.
3,
Ta có ÐMEC = 900 (nội tiếp chắn nửa đường tròn (O)) => ÐMEB = 900.
Tứ giác AMEB có ÐMAB = 900 ; ÐMEB = 900 => ÐMAB + ÐMEB = 1800 mà đây là hai góc đối nên tứ giác AMEB nội tiếp một đường tròn => ÐA2 = ÐB2 .
Tứ giác ABCD là tứ giác nội tiếp => ÐA1= ÐB2( nội tiếp cùng chắn cung CD)
=> ÐA1= ÐA2 => AM là tia phân giác của góc DAE (2)
Từ (1) và (2) Ta có M là tâm đường tròn nội tiếp tam giác ADE

a: Xét tứ giác CAOM có
góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
b: Xét (O) có
CA,CM là tiêp tuyến
nên CA=CM và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CM*MD=OM^2
=>CA*BD=R^2
c: CA=CM
OA=OM
=>CO là trung trực của AM
=>CO vuông góc với AM
=>CO//BK
Xét ΔABK có
O là trung điểm của AB
OC//BK
Do đó: C là trung điểm của AK

c.
\(CM=AC\) (t/c 2 tiếp tuyến cắt nhau) (1)
\(\widehat{KMC}=\widehat{DMB}\) (đối đỉnh)
Mà \(DM=DB\) (t/c 2 tiếp tuyến cắt nhau) \(\Rightarrow\Delta DMB\) cân tại D
\(\Rightarrow\widehat{DMB}=\widehat{DBM}\Rightarrow\widehat{KMC}=\widehat{DBM}\)
Lại có: \(\widehat{DBM}=\widehat{AKB}\) (cùng phụ \(\widehat{ABK}\))
\(\Rightarrow\widehat{KMC}=\widehat{AKB}\Rightarrow\Delta CKM\) cân tại C
\(\Rightarrow CK=CM\) (2)
(1);(2) \(\Rightarrow CK=CA\) hay C là trung điểm AK
d.
Qua A kẻ đường thẳng song song BM cắt BD kéo dài tại E
\(\Rightarrow AKBE\) là hbh (2 cặp cạnh đối song song)
\(\Rightarrow\) 2 đường chéo KE và AB cắt nhau tại trung điểm O của AB
Hay K, O, E thẳng hàng
Theo t/c 2 tiếp tuyến ta có \(OD\perp BM\) \(\Rightarrow OD\perp AE\)
Đồng thời \(AB\perp DE\) (gt)
\(\Rightarrow\) O là trực tâm tam giác ADE
\(\Rightarrow OE\perp AD\)
\(\Rightarrow OK\perp AD\)

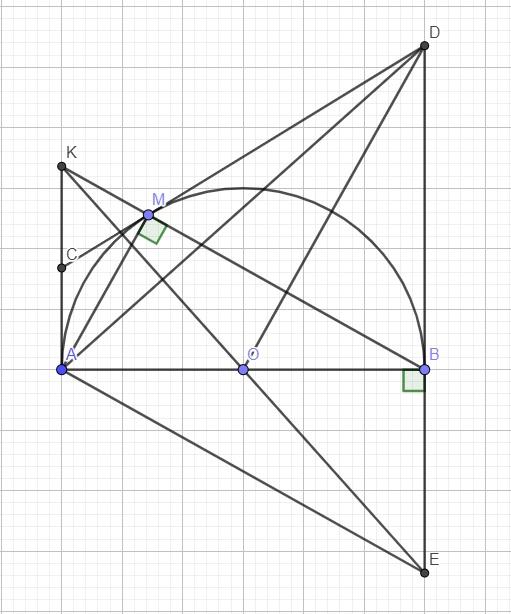
a: Xét tứ giác CAOK co
góc CAO+góc CKO=180 độ
nên CAOK là tứ giác nội tiếp
b: Xét (O) có
CK,CA là tiếp tuyến
nên CK=CA và OC là phân giác của góc AOK(1)
Xét (O) có
DK,DB là tiếp tuyến
nên DK=DB và OD là phân giác của góc KOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
OK^2=KC*KD
=>AC*BD=R^2 ko đổi
c: Xét ΔOAK có OA=OK=AK
nên ΔOAK đều
=>gócc AOK=60 độ
=>góc KOB=120 độ
=>góc KDB=60 độ
mà DK=DB
nên ΔDKB đều

a) Để chứng minh CM PQ = PN + NQ, ta sẽ sử dụng định lí Pitago trong tam giác vuông.
Gọi A là giao điểm của tiếp tuyến Mx và Ny. Ta có tam giác AMP và tam giác ANQ là tam giác vuông tại M và N.
Theo định lí Pitago, ta có:
AM^2 = AP^2 + PM^2
AN^2 = AQ^2 + NQ^2
Vì tam giác AMP và tam giác ANQ là tam giác vuông, nên ta có:
AP = AM - PM
AQ = AN - NQ
Thay vào các công thức trên, ta có:
AM^2 = (AM - PM)^2 + PM^2
AN^2 = (AN - NQ)^2 + NQ^2
Mở ngoặc và rút gọn, ta có:
AM^2 = AM^2 - 2AM*PM + PM^2 + PM^2
AN^2 = AN^2 - 2AN*NQ + NQ^2 + NQ^2
Simplifying, we have:
2AM*PM = 2AN*NQ
Chia cả hai vế cho 2, ta có:
AM*PM = AN*NQ
Vì AM = AN (vì là đường kính của nửa đường tròn), nên ta có:
PM = NQ
Do đó, ta có:
PQ = PM + NQ
Vậy, CM PQ = PN + NQ đã được chứng minh.
b) Để chứng minh CM góc PIO = 90 độ, ta sẽ sử dụng tính chất của tiếp tuyến và tiếp tuyến chung.
Gọi O là tâm của nửa đường tròn. Ta có:
Góc PIO = Góc PIM + Góc MIO
Vì PM là tiếp tuyến của đường tròn tại M, nên góc PIM = 90 độ.
Vì Mx và Ny là tiếp tuyến chung, nên góc MIO = góc NIO.
Vậy, góc PIO = 90 độ đã được chứng minh.
c) Để chứng minh CM MN là tiếp tuyến của đường tròn đường kính PQ, ta sẽ sử dụng tính chất của tiếp tuyến và góc chóp đồng quy.
Gọi O là tâm của nửa đường tròn. Ta có:
Góc MON = Góc MOP + Góc NOP
Vì MN là tiếp tuyến của đường tròn tại M, nên góc MOP = 90 độ.
Vì Mx và Ny là tiếp tuyến chung, nên góc NOP = góc NMO.
Vậy, góc MON = 90 độ.
Do đó, MN là tiếp tuyến của đường tròn đường kính PQ đã được chứng minh.




a: Xét (O) có
EA,EM là tiếp tuyến
=>EA=EM và OE là phân giác của góc AOM(1)
Xét (O) có
FA,FN là tiếp tuyến
=>FA=FN và OF là phân giác của góc AON(2)
Từ (1), (2) suy ra góc EOF=1/2*180=90 độ
b: EF=EA+AF
=>EF=EM+FN
c: góc EFO=90-60=30 độ
Bạn ơi cho mình hỏi EOF có phải tính k a