Tìm x, biết:
2x3 + 5x2 + x - 2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 6 2023
a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21
NT
1
14 tháng 4 2021
a) Ta có: B(x)-M(x)=A(x)
nên M(x)=B(x)-A(x)
\(=x^4-2x^3+5x^2+x+10-x^4-2x^3+5x^2+3x+6\)
\(=-4x^3+10x^2+4x+16\)
ND
5
A
18 tháng 8 2020
\(a\left(x\right)=5x^4-3x^2-2x^3+4-5x^4+5x^2-x+2x^3+1\)
\(=2x^2+4-x\)
Bậc : 2
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
18 tháng 8 2020
\(a\left(x\right)=5x^4-3x^2-2x^3+4-5x^4+5x^2-x+2x^3+1\)
\(a\left(x\right)=\left(5x^4-5x^4\right)+\left(2x^3-2x^3\right)+\left(5x^2-3x^2\right)-x+\left(4+1\right)\)
\(a\left(x\right)=2x^2-x+5\). Bậc của \(a\left(x\right)\) là 2
LM
1
15 tháng 12 2021
\(a,=\left(2x^3-x^2+x+4x^2-2x+2-x+1\right):\left(2x^2-x+1\right)\\ =\left[x\left(2x^2-x+1\right)+2\left(2x^2-x+1\right)-x+1\right]:\left(2x^2-x+1\right)\\ =x+2\left(\text{dư }-x+1\right)\\ b,=\left[x^2\left(2x-5\right)+3\left(2x-5\right)\right]:\left(2x-5\right)\\ =x^2+3\)
PT
1
CM
22 tháng 3 2018
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
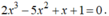
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
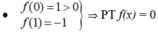có ít nhất một nghiệm c1 ∈ (0;1).
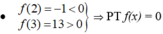có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.
20 tháng 10 2021
a: \(5x^2\left(3x^3-2x^2+x+2\right)\)
\(=15x^5-10x^4+5x^3+10x^2\)
b: \(3x^4\left(-2x^3+5x^2-\dfrac{2}{3}x+\dfrac{1}{3}\right)\)
\(=-6x^7+15x^6-2x^5+x^4\)
2x3 + 5x2 + x - 2 = 0
<=> 2x3 + 2x2 + 3x2 + 3x - 2x - 2 = 0
<=> 2x2(x + 1) + 3x(x + 1) - 2(x + 1) = 0
<=> (x + 1)(2x2 + 3x - 2) = 0
<=> (x + 1)(2x2 + 4x - x - 2) = 0
<=> (x + 1)[2x(x + 2) -(x + 2)] = 0
<=> (x + 1)(x + 2)(2x - 1) = 0
<=> x + 1 = 0 hay x + 2 = 0 hay 2x - 1 = 0
<=> x = -1 x = -2 2x = 1
<=> x = 1/2