Khi phóng tia lửa điện qua các nguyên tử hydrogen ở áp suất thấp, các electron bị kích thích lêntrạng thái năng lượng cao hơn. Sau đó, electron nhanh chóng chuyển về mức năng lượng cơ bản (n = 1) và bức xạ ra photon với các bước sóng khác nhau tạo thành dãy phổ. Tính bước sóng (λ, nm) nhỏ nhất và bước sóng lớn nhất theo nm của dãy phổ nếu electron chuyển từ n > 1 về n = 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Năng lượng của phôtôn phát ra khi electron chuyển từ trạng thái dừng E N về trạng thái trong (x) là ε = E N - E x , ε lớn nhất khi E x nhỏ nhất (ứng với trạng thái cơ bản), suy ra năng lượng lớn nhất của photon phát ra là ε = ε 0

Đáp án: A
Năng lượng mà nguyên tử hiđro nhận:
W = W2 – W1 = - 13,6/4 (eV) – (- 13,6) (eV) = 10,2 (eV)
Động năng của electron sau va chạm là:
Wđ = 12,6 (eV) – 10,2 (eV) = 2,4 (eV).

Đáp án D
*Động năng còn lại của electron:
![]()
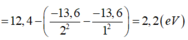
Chú ý: Trạng thái kích thích thứ nhất ứng với n = 2.

Chọn đáp án D
W = W 0 − Ε n − Ε 1 = 12 , 4 − − 13 , 6 2 2 − − 13 , 6 1 2 = 2 , 2 e V
Chú ý: Trạng thái kích thích thứ nhất ứng với n = 2
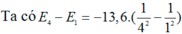
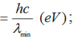
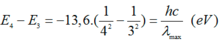
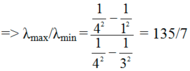
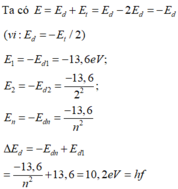

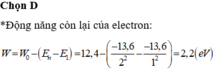
\(\lambda_{max}=\dfrac{hc}{13,6\left(\dfrac{1}{1}-\dfrac{1}{2^2}\right)eV\cdot1,602\cdot10^{-19}J\cdot eV^{-1}}m\cdot10^9nm\cdot m^{-1}=121,56nm\\ \lambda_{min}=\dfrac{hc}{13,6\left(\dfrac{1}{1}-\dfrac{1}{n_{\infty}^2}\right)eV\cdot1,602\cdot10^{-19}J\cdot eV^{-1}}m\cdot10^9nm\cdot m^{-1}=91,17nm\)