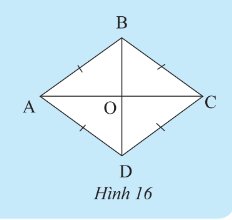
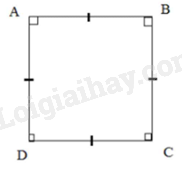
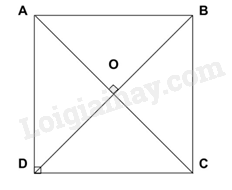
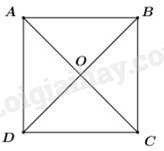
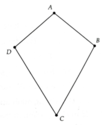
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)