Chứng minh đẳng thức \({\left( {10a + 5} \right)^2} = 100a\left( {a + 1} \right) + 25\). Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính \({25^2};{35^2}\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
19 tháng 4 2017
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
NN
19 tháng 4 2017
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5 :
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng :
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
MT
29 tháng 5 2015
\(\left(10a+5\right)^2=\left(10a\right)^2+2.10a.5+5^2=100a^2+100a+25\)
\(=100\left(a+1\right)+25\)(đpcm)
suy ra công thức bình phương của một số tân cùng bằng 5
CM
3 tháng 2 2019
Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
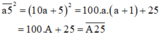
Do vậy, để tính bình phương của một số tự nhiên có dạng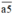 
, ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
Áp dụng:
252 = 625 (Vì 2.3 = 6)
352 = 1225 (Vì 3.4 = 12)
652 = 4225 (Vì 6.7 = 42)
752 = 5625 (Vì 7.8 = 56)
CB
11 tháng 2 2017
Bài giải:
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
CB
11 tháng 2 2017
Bài giải:
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
18 tháng 9 2018
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng:
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
652 = 4225
752 = 5625
25 tháng 10 2020
Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
Do vậy, để tính bình phương của một số tự nhiên có dạng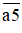 
, ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
12 tháng 9 2020
Ta có thể chứng minh bằng cách sau:
(10a+5)^2=(10a)^2+10.5.2.a+5^2
=100a^2+100.a+25
=100a*(a+1)+25
\(\begin{array}{l}VT = {\left( {10a + 5} \right)^2} = {\left( {10a} \right)^2} + 2.10a.5 + {5^2} = 100{a^2} + 100a + 25\\ = \left( {100{a^2} + 100a} \right) + 25 = 100a\left( {a + 1} \right) + 25 = VP\end{array}\)
Vậy \({\left( {10a + 5} \right)^2} = 100a\left( {a + 1} \right) + 25\).
Quy tắc: Muốn tính bình phương một số có tận cùng bằng 5, ta nhân 100 với tích số chục và số liền sau số chục rồi cộng với 25.
Áp dụng:
\(\begin{array}{l}{25^2} = 100.2.3 + 25 = 600 + 25 = 625;\\{35^2} = 100.3.4 + 25 = 1200 + 25 = 1225.\end{array}\)