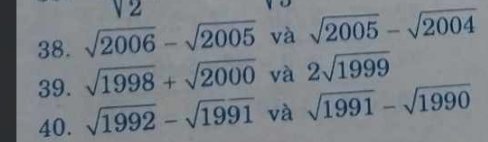Question

[hoang thi thi]

giúm mình bài này v ạ so sánh ạ mình camon

Answer 1

[Akai Haruma]

38.

$\sqrt{2006}-\sqrt{2005}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{\sqrt{2006}+\sqrt{2005}}< \frac{1}{\sqrt{2005}+\sqrt{2004}}=\frac{2005-2004}{\sqrt{2005}+\sqrt{2004}}=\sqrt{2005}-\sqrt{2004}$

Answer 2

[Akai Haruma]

39.

$\sqrt{1998}+\sqrt{2000}-2\sqrt{1999}=(\sqrt{2000}-\sqrt{1999})-(\sqrt{1999}-\sqrt{1998})$

$=\frac{1}{\sqrt{2000}+\sqrt{1999}}-\frac{1}{\sqrt{1999}+\sqrt{1998}}$

$< 0$

$\Rightarrow \sqrt{1998}+\sqrt{2000}<2\sqrt{1999}$

Bài 40 bạn làm tương tự câu 38.