trên cạnh AB của hình chữ nhật ABCD lấy điểm M và N sao cho AM = BN ( M nằm giữa A và N ) Chứng minh MNCD là hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


các bạn giúp mình với, nhớ làm bài giải nhé.
giúp mình đi, mình k cho

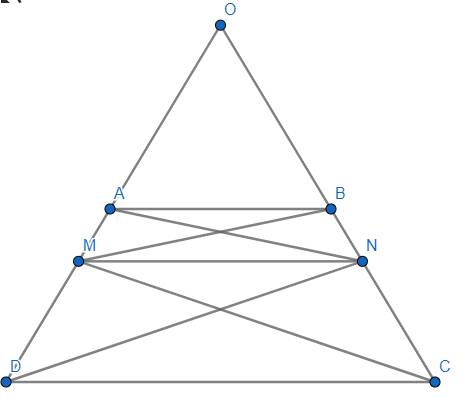
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).
Xét Δ ADM và Δ BNC ta có :
Góc A = Góc B = 90o (ABCD là HCN)
AD=BC (ABCD là HCN)
AM=BN (đề bài)
⇒ Δ ADM và Δ BNC (cạnh, góc, cạnh)
⇒ Góc ADM = Góc BCN
mà Góc ADM + Góc MDC =90o
Góc BCN + Góc NCD =90o
⇒ Góc MDC = Góc NCD
mà MN song song CD (AB song song CD)
⇒ MNCD là hình thang cân